Consider three quantities: x=EB,y=1√μ0ε0,andz=lCR.
Here , l is the length of a wire , C is the capacitance , and R is a resistance. All other symbols have usual meanings. Then
x, y and z have the same dimension
only x and z have the same dimension
only x and y have the same dimension
Only y and z have the same dimension
To solve the problem, we need to find the dimensions of the three quantities x, y, and z.
Step 1: Find the dimensions of x=EB
1. Electric Field E: The electric field is defined as the force per unit charge. The dimensions of force are (MLT−2) and charge has dimensions (IT). Therefore, the dimensions of electric field E are:
(E)=(F)(q)=(MLT−2)(IT)=(MLT−3I−1)
2. Magnetic Field B: The magnetic field is defined in terms of the force experienced by a charge moving in the field. The dimensions of magnetic field B can be derived from the Lorentz force law:
F=q(v×B)⟹(B)=(F)(q)(v)=(MLT−2)(IT)(LT−1)=(MT−2I−1)
3. Calculate x:
x=EB=(MLT−3I−1)(MT−2I−1)=(LT−1)
Step 2: Find the dimensions of y=1√μ0ϵ0
1. Permeability μ0: The dimensions of permeability can be derived from the relation involving magnetic field and current:
(μ0)=(F)(I2)=(MLT−2)(I2)=(MLT−2I−2)
2. Permittivity ϵ0: The dimensions of permittivity can be derived from the relation involving electric field and charge:
(ϵ0)=(Q)(V2)=(IT)(MLT−3I−1)2=(M−1L−2T4I2)
3. Calculate y:
y=1√μ0ϵ0=1√(MLT−2I−2)⋅(M−1L−2T4I2)=1√(L−1T2)=(LT−1)
Step 3: Find the dimensions of z=lCR
1. Resistance R: From Ohm's law, V=IR, we have:
(R)=(V)(I)=(ML2T−3I−1)(I)=(ML2T−3I−2)
2. Capacitance C: From the relation Q=CV:
(C)=(Q)(V)=(IT)(ML2T−3I−1)=(M−1L−2T4I2)
3. Calculate z:
z=lCR=(L)(M−1L−2T4I2)⋅(ML2T−3I−2)=(LT−1)
Conclusion
All three quantities x, y, and z have the same dimensions:
(x)=(y)=(z)=(LT−1)
Thus, the correct option is that xyz have the same dimension.
---
(E)=(F)(q)=(MLT−2)(IT)=(MLT−3I−1)
F=q(v×B)⟹(B)=(F)(q)(v)=(MLT−2)(IT)(LT−1)=(MT−2I−1)
x=EB=(MLT−3I−1)(MT−2I−1)=(LT−1)
(μ0)=(F)(I2)=(MLT−2)(I2)=(MLT−2I−2)
(ϵ0)=(Q)(V2)=(IT)(MLT−3I−1)2=(M−1L−2T4I2)
y=1√μ0ϵ0=1√(MLT−2I−2)⋅(M−1L−2T4I2)=1√(L−1T2)=(LT−1)
(R)=(V)(I)=(ML2T−3I−1)(I)=(ML2T−3I−2)
(C)=(Q)(V)=(IT)(ML2T−3I−1)=(M−1L−2T4I2)
z=lCR=(L)(M−1L−2T4I2)⋅(ML2T−3I−2)=(LT−1)
(x)=(y)=(z)=(LT−1)
Topper's Solved these Questions
Similar Questions
Consider three quantities (x= E/B, y= (sqrt(1/((mu_0)(epsilon_0)))) and z=(1/CR)'. Here, l is the length of a wire, C is a capacitance and R is a resistance. All other symbols have standard meanings.
View SolutionDimension of 1μ0ε0, where symbols have usual meaning, are
View SolutionThe dimension of e2/ε0hc (here symbols have their usual meanings) are
View SolutionWhat is the dimensional formula of 1μ0ε0 where the symbols have their usual meanings?
View SolutionIn a series L-C-R, AC circuit assuming that symbols have their usual meanings match the following two columns.
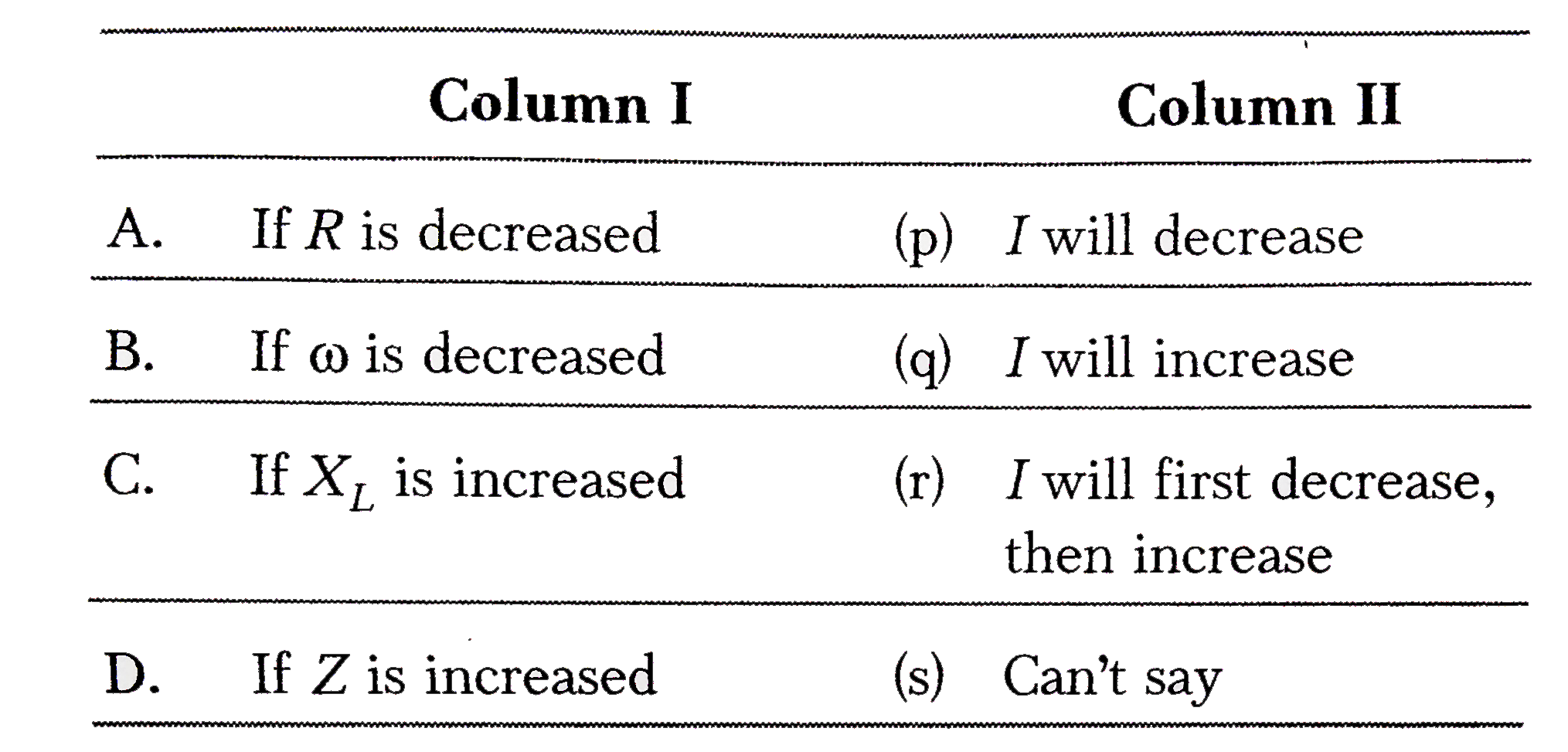
View SolutionL, C and R represent the physical quantities, inductance, capacitance and resistance respectively. The combination(s) which have the dimensions of frequency are
View SolutionL, C and R represent the physical quantities inductance, capacitance and resistance respectively. The combinations which have the dimensions of frequency are-
View SolutionL, C and R represent the physical quantities, inductance, capacitance and resistance respectively. The combination(s) which have the dimensions of frequency are
View SolutionIn a ΔABC, if b=(√3−1)aand∠C=30∘, then the value of (A-B) is equal to (All symbols used have usual meaning in the triangel.)
View SolutionWhich of the following pairs have the same dimensions ?
(L = inductance , C = capacitance , R = resistance)
View Solution
