A solid horizontal surface is coovered with a thin layer of oil.A rectangular block of mass m = 0.4 kg is at rest on this surface. An impulse of 1.0 N s is applied to the block at time to t = 0 so that it starts moving along the x-axis with a velocity v(t)=v0e=t/τ , where v0 is a contant and τ=4s.The displacement of the block, in metres, at t=τ is ................... Take e−1=0.37 ?
Step by step video & image solution for A solid horizontal surface is coovered with a thin layer of oil.A rectangular block of mass m = 0.4 kg is at rest on this surface. An impulse of 1.0 N s is applied to the block at time to t = 0 so that it starts moving along the x-axis with a velocity v(t) =v_(0)e^(=t//tau) , where v_(0) is a contant and tau = 4s.The displacement of the block, in metres, at t = tau is "..................." Take e^(-1) = 0.37 ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
A particle located at x=0 at time t=0, starts moving along with the positive x−direction with a velocity 'v' that varies as v=a√x. The displacement of the particle varies with time as
At2BtCt12Dt3A particle located at x = 0 at time t = 0, starts moving along the positive x-direction with a velocity that varies as v=p√x. The displacement of the particle varies with time as (where, p is constant)
At3Bt2CtDt1/2A block of mass 2 kg rests on a horizontal surface. If a horizontal force of 5 N is applied on the block, the frictional force on it is (take,uk=0.4,μs=0.5)
A5NB10NC8NDzero
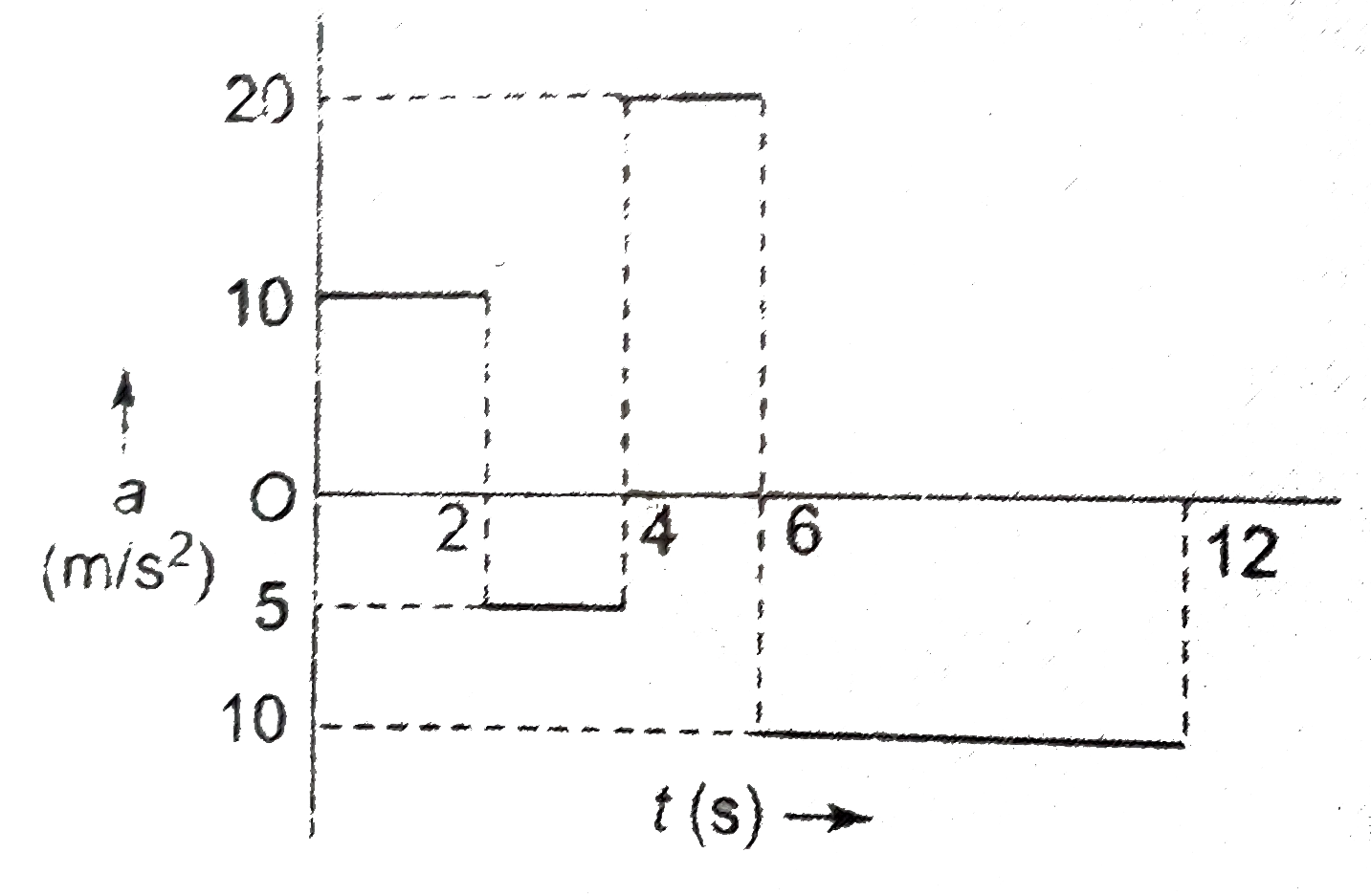
A particle is moving along the x-axis. Consider it’s a-t graph. If initial velocity is 10 m//s, sketch the v-t graph and calculate the displacement in the time interval t=0 to 12 s.
View SolutionThe velocity v of a body moving along a straight line varies with time t as v=2t2e−t, where v is in m/s and t is in second. The acceleration of body is zero at t =
View SolutionA uniform cube of mass m and edge a moves on a horizontal surface along the positive x-axis, with initial velocity v0. Then
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The displacement of aprticle from t=0 to t=2 seconds is :
View SolutionThe position of a particle at time t is given by the relation x(t)=v0A(1−e−At), where v0 is constant and A>0. The dimensions of v0 and A respectively
View Solution

