A particle of mass 3 kg is moving along x - axis and its position at time t is given by equation x=(2t2+5)m. Work done by all the force acting on it in time interval t=0 to t=3s is
144 J
72 J
108 J
216 J
The correct Answer is:D
To find the work done by all the forces acting on a particle of mass 3 kg moving along the x-axis, we can follow these steps:
Step 1: Determine the position function
The position of the particle is given by the equation:
x(t)=2t2+5 m
Step 2: Differentiate the position function to find velocity
To find the velocity v(t), we differentiate the position function x(t) with respect to time t:
v(t)=dxdt=ddt(2t2+5)=4t m/s
Step 3: Differentiate the velocity function to find acceleration
Next, we differentiate the velocity function v(t) to find the acceleration a(t):
a(t)=dvdt=ddt(4t)=4 m/s2
Step 4: Calculate the force acting on the particle
Using Newton's second law, the force F acting on the particle can be calculated as:
F=m⋅a
Given that the mass m=3 kg and a=4 m/s2:
F=3 kg⋅4 m/s2=12 N
Step 5: Calculate the work done over the time interval
The work done W by the force over a displacement can be calculated using the formula:
W=F⋅d
where d is the total displacement over the time interval from t=0 to t=3 seconds.
Step 6: Find the displacement over the time interval
To find the displacement, we evaluate the position function at t=3 and t=0:
- At t=3:
x(3)=2(32)+5=2(9)+5=18+5=23 m
- At t=0:
x(0)=2(02)+5=5 m
Thus, the total displacement d is:
d=x(3)−x(0)=23 m−5 m=18 m
Step 7: Calculate the work done
Now we can calculate the work done using the force and the displacement:
W=F⋅d=12 N⋅18 m=216 J
Final Answer
The work done by all the forces acting on the particle in the time interval from t=0 to t=3 seconds is:
216 J
The position of the particle is given by the equation:
x(t)=2t2+5 m
To find the velocity v(t), we differentiate the position function x(t) with respect to time t:
v(t)=dxdt=ddt(2t2+5)=4t m/s
Next, we differentiate the velocity function v(t) to find the acceleration a(t):
a(t)=dvdt=ddt(4t)=4 m/s2
Using Newton's second law, the force F acting on the particle can be calculated as:
F=m⋅a
Given that the mass m=3 kg and a=4 m/s2:
F=3 kg⋅4 m/s2=12 N
The work done W by the force over a displacement can be calculated using the formula:
W=F⋅d
where d is the total displacement over the time interval from t=0 to t=3 seconds.
To find the displacement, we evaluate the position function at t=3 and t=0:
- At t=3:
x(3)=2(32)+5=2(9)+5=18+5=23 m
- At t=0:
x(0)=2(02)+5=5 m
d=x(3)−x(0)=23 m−5 m=18 m
Now we can calculate the work done using the force and the displacement:
W=F⋅d=12 N⋅18 m=216 J
The work done by all the forces acting on the particle in the time interval from t=0 to t=3 seconds is:
216 J
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - A)
67 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)
39 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)
14 Videos
- WAVESBOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
The position (x) of a particle of mass 1 kg moving along X-axis at time t is given by (x=12t2) metre. Find the work done by force acting on it in time interval from t=0 to t=3s.
View SolutionThe position (x) of a particle of mass 2 kg moving along x-axis at time t is given by x=(2t3) metre. Find the work done by force acting on it in time interval t=0 to t=2 is :-
View Solution
Knowledge Check
The position (x) of a particle of mass 1 kg moving along X-axis at time t is given by (x=12t2) metre. Find the work done by force acting on it in time interval from t=0 to t=3s.
A4.2 JB5.4 JC4.6 JD4.5 JA particle of mass 10 kg is moving in a straight line. If its displacement, x with time tis given by x=(t3−2t−10)m then the force acting on it at the end of 4 seconds is
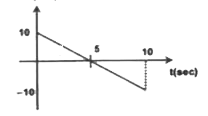
A24NB240NC300ND1200NThe velocity-time graph of a particle moving in a straight line is shown in figure. The mass of the particle is 2kg. Work done by all the forces acting on the particle in time interval between t=0 to t=10s is
 A(a) 300JB(b) −300JC(c) 400JD(d) −400J
A(a) 300JB(b) −300JC(c) 400JD(d) −400J
The displacement of a body of mass 2kg varies as S=t2+2t .Where S is in meters and t is in second.The work done by all the forces acting on the body during the time interval t=0 to t=3s is ?
View SolutionA particle of mass 1 kg is moving along X - aixs . Its X - coordinate is given by x=t2 . Where t is in secoonds and x in metres . Find the work done by thef orce on the particle in time interval t = 1s to t = 3 s .
View SolutionVelocity-time graph of a particle moving in a straight line is shown in the figure. Mass of the particle is 2 kg. Work done by all the forces acting on the particle in time interval t = 0 to t = 10 sec is
View SolutionA point mass of 0.5 kg is moving along x− axis as x=t2+2t , where, x is in meters and t is in seconds. Find the work done (in J) by all the forces acting on the body during the time interval [0,2s].
View SolutionThe displacement of a body of mass 2 kg varies with time t as S=t2+2t, where S is in m and t is in s. The work done by all the forces acting on the body during the time interval t=2 to t=4 s is
View Solution
