A horizontal plank is 10.0m long with uniform density and mass 10kg .It rests on two supports which are placed 1.0m from each end as shown in the figure. A man of mass 80 kg can stand upto distance x on the plank without causing it to tip .The value of x is
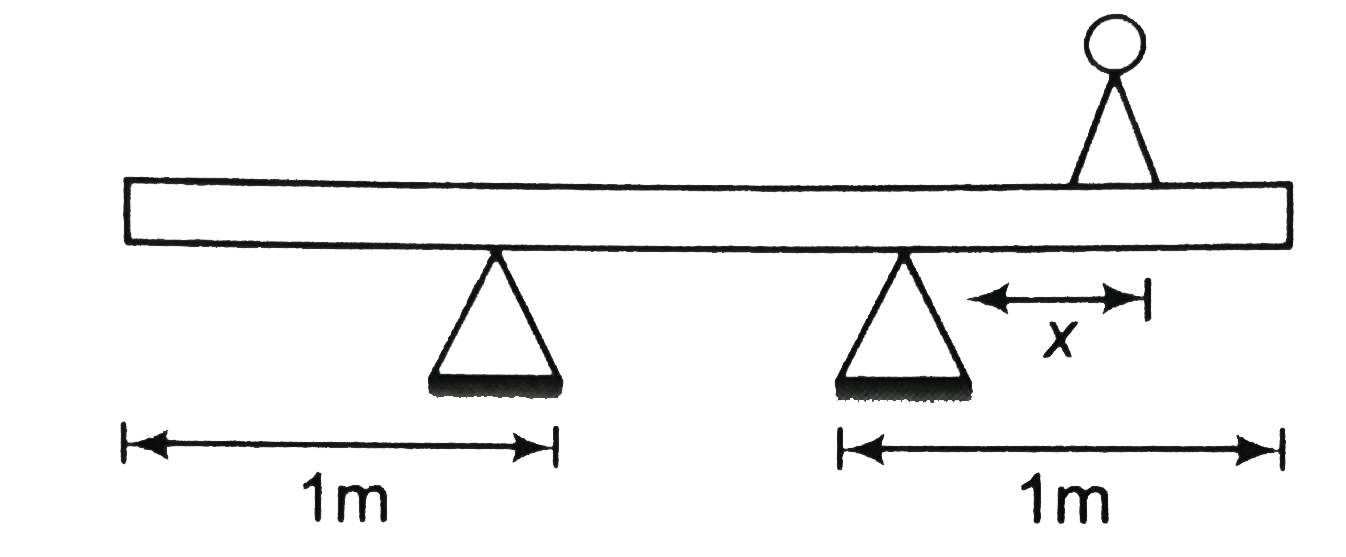
12m
14m
34m
18m
The correct Answer is:A
just at the time of tipping , normal reation at 1 will become zero
∑(moments of all forces about point 2)=0
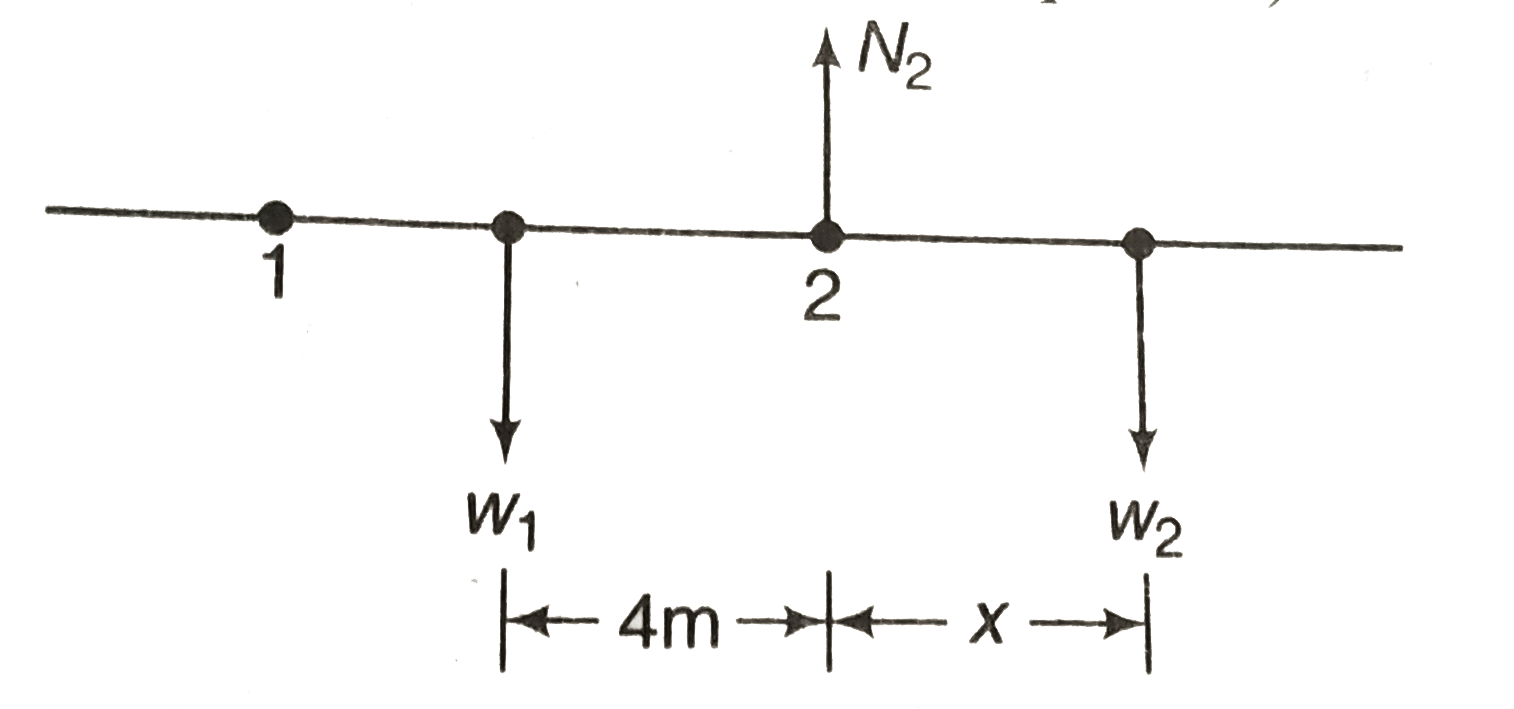
∴W1(4)=w2(x)
or x=4w1w2=4(10g)80g=12m
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question32videos
LAWS OF MOTION
- BOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension9videos
LAWS OF MOTION
- BOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.52videos
LAWS OF MOTION
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
- BOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective18videos
LAWS OF THERMODYNAMICS
Similar Questions
A uniform rod of mass M and length L rests on two supports. A ball of mass m=M/3 is placed at distance L/8 from the center as shown. Find reactions at supports.
 View Solution
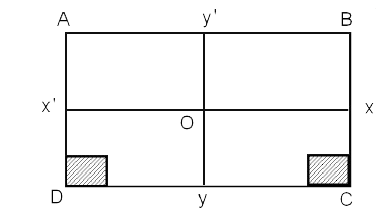
View SolutionA uniform square plate ABCD has a mass of 10kg. If two point masses of 3 kg each are placed at the corners C and D as shown in the adjoining figure, then the centre of mass shifts to the point which is lie on -
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform wooden plank of mass 150 kg and length 8 m is floating on still water with a man of 50 kg at one end of it . The man walks to the other end of the plank and stops. Than the distance covered by the plank is
A1 mB4 mC2 mDZero - Question 2 - Select One
Two painters are working from a wooden hoard 5m long suspended from the top of a building by two ropes attached to the ends of the plank. Either rope can withstand a maximum tension of 1040N. Painter A of mass 80kg is working at a distance of 1m from one end. Painter B of mass 60kg is working at a distance of x in from the centre of mass of the board on the other side. Take mass of the board as 20kg and g=10ms−2. The range of x so that both the painters can work safely is
A13<x<116B0<x<116C0<x<2D13<x<2 - Question 3 - Select One
A man of mass m stands at the left end of a uniform plank of length L and mass M, which lies on a frictionaless surface of ice. If the man walks to the other end of the plank, then by what distance does the plank slide on the ice?
ALBMLm+MCmLMDmLm+M

A horizontal plank having mass m lies on a smooth horizontal surface. A sphere of same mass and radius r is spined to angular frequency ω0 and gently placed on the plank as shown in the figure. If coefficient of friction between the plank and the sphere is μ. Find the distance moved by the plank till sphere starts pure rolling on the plank. the plank is long enough.View SolutionA uniform board of mass M and length L rests on two spring scales. A person of mass m stands at a distance l from one end as shown in Fig. (a) The board and person are at rest. What is the reading of the two scales?
View SolutionA plank of mas M and length L is at rest on as frictionless floor. The top surface of the plank has friction. At one end of it a man of mass m is standing as shown in figure. If the man walks towards the other end the find the distance, which the plank moves a till the man reaches the centre of the plank. b. till the man reaches the other end of the plank.
 View Solution
View SolutionA block of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
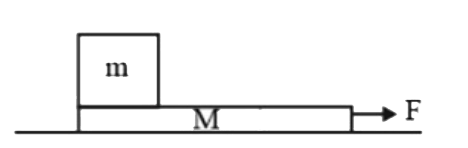 View Solution
View SolutionWhich of the following statements are true ?
(i) A uniform wooden plank of mass 150kg and length 8m is floating on still water with a man of 50kg at one end of it. The man walks to the other end of the plank and stops. The distance covered by the plank is 2m.
(ii) A kid of mass 15kg is sitting in a boat of mass 45kg in a lake. The distance of kid from the bank of lake is 12m. Now the body moves inside the boat at a distance 4m towards the bank and stops. The distance of the kid from the bank (there is no friction between the water and the boat ) is 11m.
(iii) Two persons of masses 40kg and 60kg are sitting at the midpoint of a 12−m- long boat (140kg) standing still in water. Now they move to opposite ends of the boat. Neglecting the friction between boat and water, the distance traveled by the boat in water is 50cm.
(iv) In a gravity free space , a man of mass m standing at a height h above the floor, throws a ball of mass m0 straight down with a speed v0. When the ball reaches the floor, the distance of the man above the floor is (1+m0m)h.View Solution

