Bernoulli's Equation

Video Solution

|

Answer

Step by step video solution for Bernoulli's Equation by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS PROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Mechanical Properties of fluidsBOOK - SL ARORACHAPTER - Mechanical Properties of fluidsEXERCISE - Exercise
459 Videos
Mathematical toolsBOOK - SL ARORACHAPTER - Mathematical toolsEXERCISE - Exercise
20 Videos
Mechanical Properties of SolidsBOOK - SL ARORACHAPTER - Mechanical Properties of SolidsEXERCISE - Example
113 Videos

Similar Questions

Knowledge Check

Statement-1 : Bernoullis equation is based on energy conservation.
Statement-2 : Bernoullis equation can only be applied if the flow is streamlined.
Statement-3 : Bernoullies equation can be applied evern if the flow is not streamlined as total energy is always conserved.
AT T T
BT F T
CT T F
DF F F
using the illustration when both surfaces 1 and 2 are exposed to the atmoshere, $P_{1}$ and $P_{2}$ are gauge pressure , and $h_{1}$ and $h_{2}$ are heights .

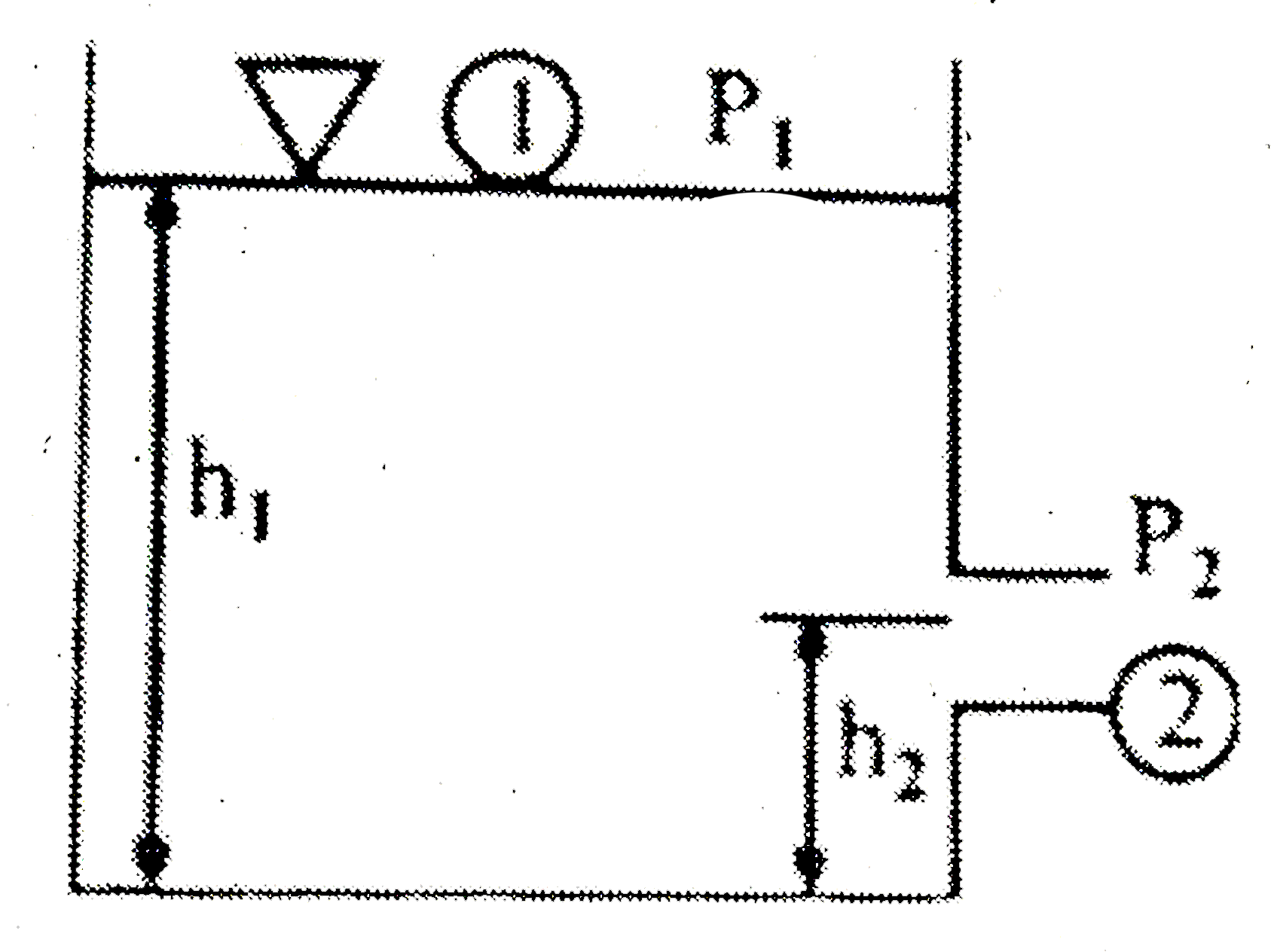
The Bernoulli equation for this situation is $h_{1} + \frac{P_{1}}{W} + \frac{V_{1}^{2}}{2a} = h_{2} + \frac{P_{2}}{W} + \frac{V_{2}^{2}}{2a}$
The velocity of the fluid leavening point (2) is constant and can be expressed as
A $V_{2} = (P_{1} / P_{2}) V_{1}$
B $V_{2} = (P_{1} / P_{2}) a h$
C $V_{2} = {[(h_{1} - h_{2}) (2 a)]}^{1 / 2}$
Dnone of the above
using the illustration when both surfaces 1 and 2 are exposed to the atmoshere, $P_{1}$ and $P_{2}$ are gauge pressure , and $h_{1}$ and $h_{2}$ are heights .

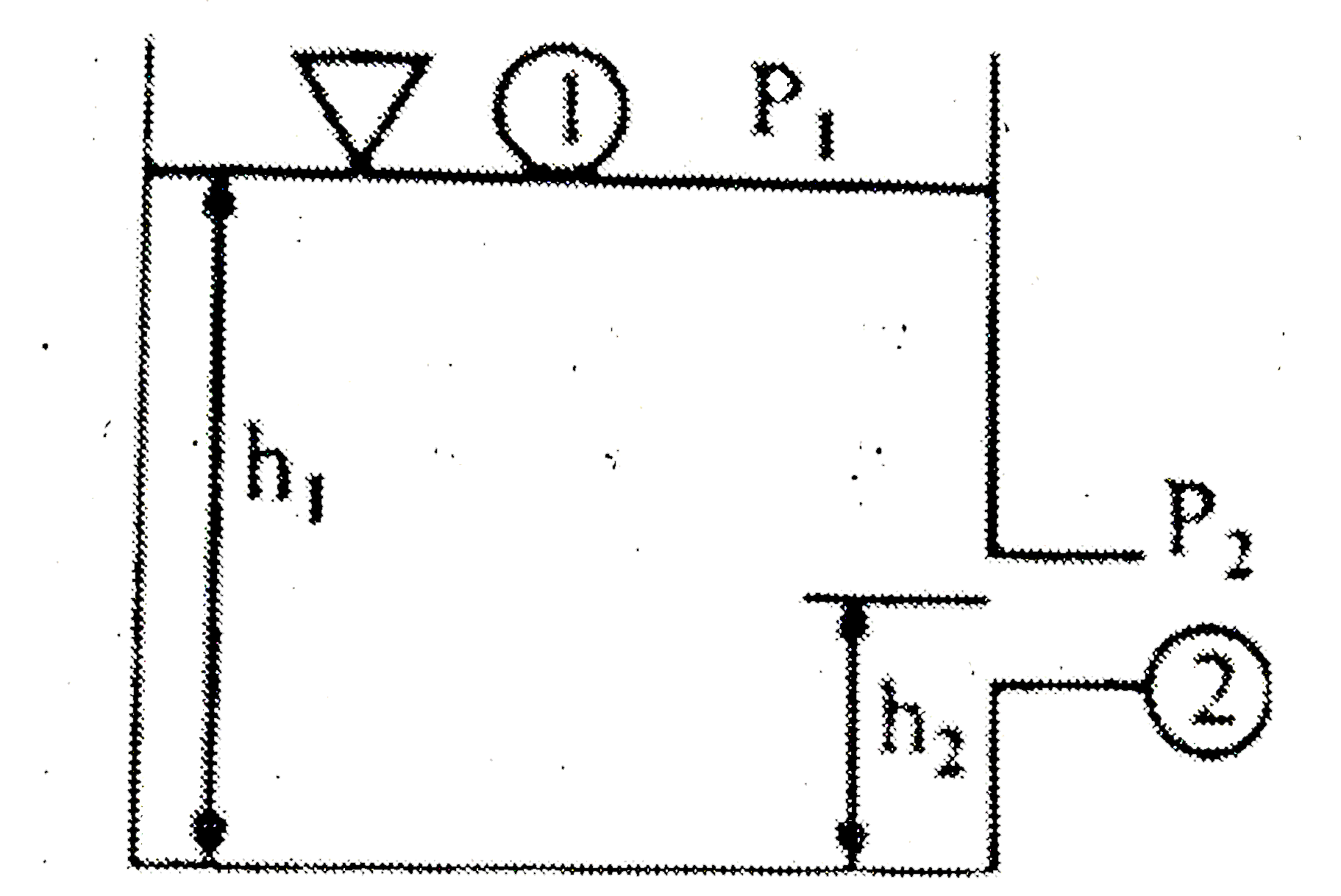
The Bernoulli equation for this situation is $h_{1} + \frac{P_{1}}{W} + \frac{V_{1}^{2}}{2a} = h_{2} + \frac{P_{2}}{W} + \frac{V_{2}^{2}}{2a}$
If an Identical outlet were placed at exactly the same point on the left side of the container, the velocity would be
Azero
Bcomputable
C $2 V_{2}$
Dnone of the above

SL ARORA-Mechanical Properties of fluids-Exercise

Home
Ask Doubt
Profile