A solid sphere having volume $V$ and density $ρ$ floats at the interface of two immiscible liquids of densites $ρ_{1}$ and $ρ_{2}$ respectively. If $ρ_{1} < ρ < ρ_{2}$ , then the ratio of volume of the parts of the sphere in upper and lower liquid is

A

$\frac{ρ - ρ_{1}}{ρ_{2} - ρ}$

B

$\frac{ρ_{2} - ρ}{ρ - ρ_{1}}$

C

$\frac{ρ + ρ_{1}}{ρ + ρ_{2}}$

D

$\frac{ρ + ρ_{2}}{ρ + ρ_{1}}$

Video Solution

|

Answer

Step by step video & image solution for A solid sphere having volume V and density rho floats at the interface of two immiscible liquids of densites rho_(1) and rho_(2) respectively. If rho_(1) lt rho lt rho_(2), then the ratio of volume of the parts of the sphere in upper and lower liquid is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS PROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

A solid uniform ball having volume V and density $ρ$ floats at the interface of two unmixable liquids as shown in the figure. The densities of the upper and the lower liquids are $ρ_{1}$ and $ρ_{2}$ respectively, such that $ρ_{1} < ρ < ρ_{2}$ . What fraction of the volume of the ball will be in the lower liquid ?

A $\frac{ρ - ρ_{2}}{ρ_{1} - ρ_{2}}$
B $\frac{ρ}{ρ_{1} - ρ_{2}}$
C $\frac{ρ_{1} - ρ}{ρ_{1} - ρ_{2}}$
D $\frac{ρ_{1} - ρ_{2}}{ρ_{2}}$
A solid uniform ball having volume V and density $ρ$ floats at the interface of two unmixible liquids as shown in Fig. 7(CF).7. The densities of the upper and lower liquids are $ρ_{1}$ and $ρ_{2}$ respectively, such that $ρ_{1} < ρ < ρ_{2}$ . What fractio9n of the volume of the ball will be in the lower liquid.

A $\frac{ρ - ρ_{2}}{ρ_{1} - ρ_{2}}$
B $\frac{ρ_{1}}{ρ_{1} - ρ_{2}}$
C $\frac{ρ_{1} - ρ}{ρ_{1} - ρ_{2}}$
D $\frac{ρ_{1} - ρ_{2}}{ρ_{2}}$
A solid sphere of radius r is floating at the interface of two immiscible liquids of densities $ρ_{1}$ and $ρ_{2} (ρ_{2} > ρ_{1})$ , half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure $= p_{0}$ and acceleration due to gravity is g):

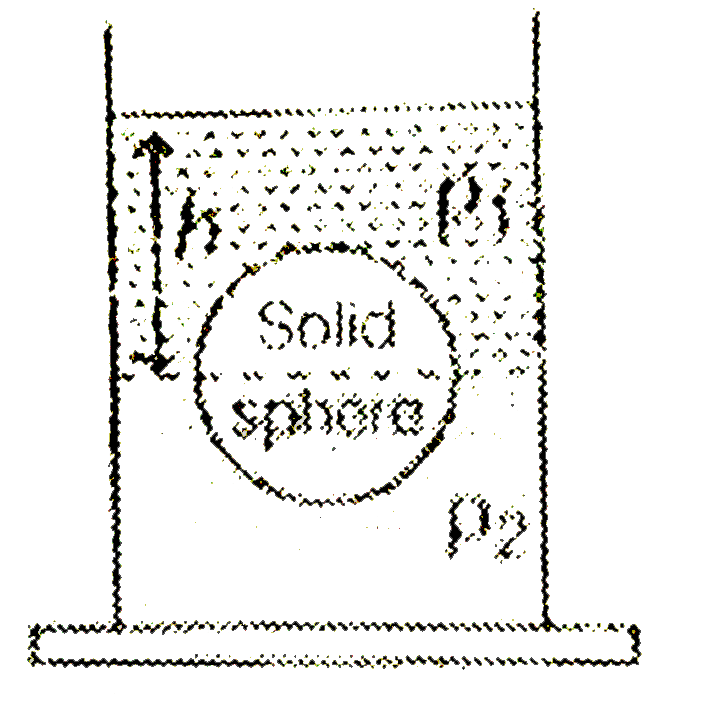A $p_{0} π r^{2} + (h - \frac{2}{3} r) π r^{2} ρ_{1} g$
B $(h - \frac{2}{3} r) π r^{2} ρ_{1} g$
C $\frac{2}{3} π r^{2} ρ_{1} g$
D $p_{0} \times π r^{2}$

SL ARORA-Mechanical Properties of fluids-Exercise

Home
Ask Doubt
Profile