The rate constant for the decompositionof N2O5 a various tempeatures is given below:

Draw a graph between in k and lT and calculate the values of A and Ea .Predict the rate constant at 30∘ and 50∘ C


Calculation of Ea:
log K2K1=−Ea2.303R(T2−T1T1T2)
According to above table,
Where ,T2=313 K so,K2=25.7×105s−1
T1=293K so, k1=1.70×105s−1
R=8.314 JK−1mol−1
log (25.7×1051.70×105)=Ea2.303×8.314(313−293313×293)
∴ log 15.1176=-Ea2.303×8.314×20313×293
∴1.1795=Ea×202.303×8.314×313×293
∴Ea=1.1795×2.303×8.314×313×29320 1.1795×87798.3-103558 J=103.558 kJ
Calculation of A on the base 293 K temperature:
Where,T=293 K,K=1.7×105
Ea=103558 J,R=8.314 JK−1mol−1
∴ log k=log A-Ea2.303RT
∴log(1.7×105)=logA−1035582.303×8.314×293
∴ 5.2304=log A-18.459
∴ log A=5.2304+18.459=23.6894
∴ A=Antilog 23.6894=4.8910×1023s−1
Calculation of A on the base of 293 K temperature:By ranging the line,it will be in =22.2,where it touches to Y-axis.
Intecept=22.2=A =In A
In A=2.303 log 22.2
∴A=(Antilog22.2)×2.303
=1.5849×1022×2.303=3.65×1022
Calculation of k at 30∘ C:
T=30+273=303K
A=4.8910×1023S−1
log k=log A=Ea2.303RT
∴ log k=log 4.8910×1023−1035582.303×8.314×303 ∴ k=Antilog 5.8394=690875.8 6909×105s−1
Calculation of k at 50∘ C:
T=50+273=323 K
∴ log k=log A-Ea2.303RT 4.8910×105−1035582.303×8.314×323 ∴ k=Antilog 6.9447=8.8044×106
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - KUMAR PRAKASHANCHAPTER - CHEMICAL KINETICSEXERCISE - Section-D (NCERT Exemplar Solution)(Multiple Choice Quetions)
20 Videos
- CHEMICAL KINETICSBOOK - KUMAR PRAKASHANCHAPTER - CHEMICAL KINETICSEXERCISE - Section-D (Multiple Choice Questions (nore than one options))
12 Videos
- CHEMICAL KINETICSBOOK - KUMAR PRAKASHANCHAPTER - CHEMICAL KINETICSEXERCISE - Section-B-(INTEXT QUESTIONS AND ANSWERS )
9 Videos
- BOARD EXAM QUESTION PAPER MARCH - 2020 BOOK - KUMAR PRAKASHANCHAPTER - BOARD EXAM QUESTION PAPER MARCH - 2020 EXERCISE - PART -B
23 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - KUMAR PRAKASHANCHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - SECTION - E (MCQs ASKED IN GUJCET/BOARD EXAM)
37 Videos
Similar Questions
The rate constant for the decomposition of N2O5 at various temperatures
is given below:
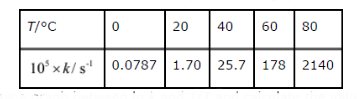
Draw a graph between ln k and 1/T and calculate the values of A and
Ea. Predict the rate constant at 30∘ and 50∘C.
View SolutionThe rate constant for the decomposition of N2O5 at various temperatures is given below:

Draw a graph beetween In k and 1/T and calculate the values of A and Ea. Predict the rate constant at 30∘ and 50∘C
View SolutionThe rate constant for the decomposition of N2O5 at various temperatures is given below:
(##KALKLCISCCHEXIIC04SLV051_Q01.png width=80%><br>Drawagraphbetweenlogkand1Tandcalca––tethevaluesofAandEq.Predicttherateconstantat30^@ C and 50^@ C.
View SolutionThe rate constant for the decomposition of N2O5 at various temperatures is given below:
(##KALKLCISCCHEXIIC04SLV051_Q01.png width=80%><br>Drawagraphbetweenlogkand1Tandcalca––tethevaluesofAandEq.Predicttherateconstantat30^@ C and 50^@ C.
View SolutionThe rate constant for the decomposition of N2O5 at various temperatures is given below:
(##KALKLCISCCHEXIIC04SLV051_Q01.png width=80%><br>Drawagraphbetweenlogkand1Tandcalca––tethevaluesofAandEq.Predicttherateconstantat30^@ C and 50^@ C.
View SolutionThe rate constant for the decomposition of N2O5 at various temperatures
is given below:

Draw a graph between ln k and 1/T and calculate the values of A and
Ea. Predict the rate constant at 30∘ and 50∘C.
View Solutionform the following data for the decompoistion of N2O5 in carbon tertrachloride solution at 321K, show that the reaction is of the first order and calculate the rate constant.
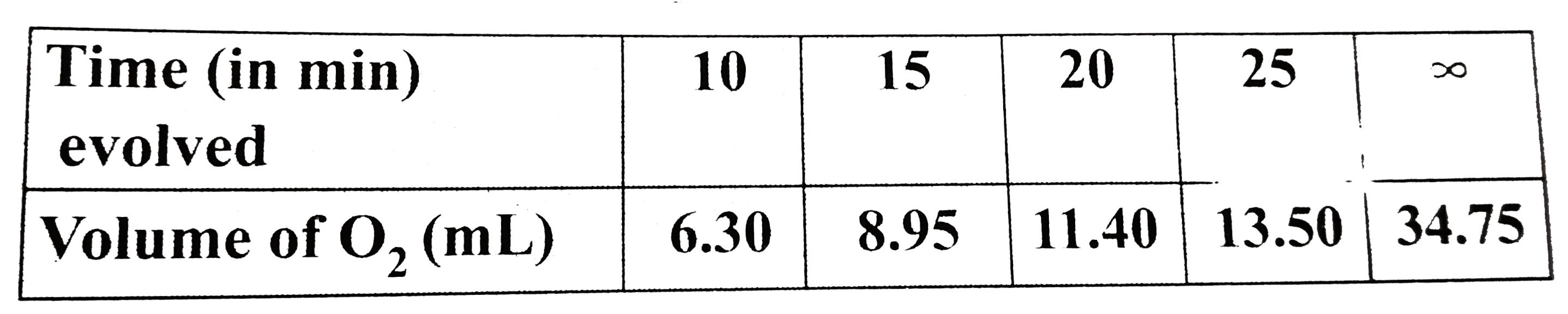
View Solutionform the following data for the decompoistion of N2O5 in carbon tertrachloride solution at 321K, show that the reaction is of the first order and calculate the rate constant.
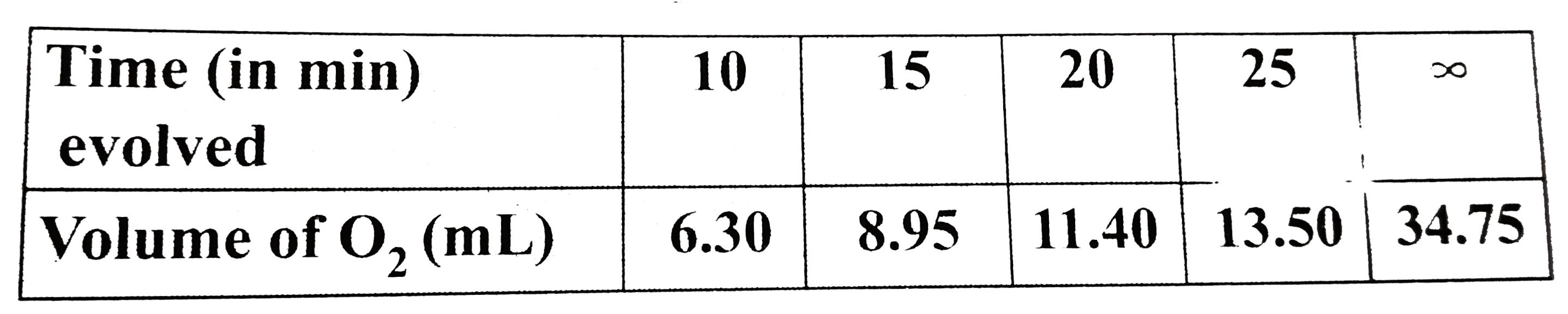
View SolutionThe rate law for the decomposition of N2O5 is given as: Rate =k[N2O5]. What is the significance of k in the equation?
View SolutionThe rate constant for the first order decomposition of N2O5 is given by the following equation: k=(2.5×1014s−1)e(−25000K)/T
Calculate Ea for this reaction and rate constant if its half-life period be 300 minutes.
View Solution
