A particle initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shwon. The particle looses its contact with hemisphere at point B. C is centre of the hemisphere. The equation relatin α and β is
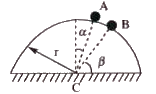
2sinα=2cosβ
2sinα=3cosβ
3sinβ=2cosα
2sinβ=3cosα
The correct Answer is:C
Topper's Solved these Questions
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - PRACTICE SHEET (EXERCISE-I WORKDONE BY FORCE) (LEVEL-I STRAIGHT OBJECTIVE TYPE QUESTIONS)
7 Videos
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - PRACTICE SHEET (EXERCISE-I WORKDONE BY FORCE) (LEVEL-II STRAIGHT OBJECTIVE TYPE QUESTIONS)
10 Videos
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - LECTURE SHEET (EXERCISE-VI POWER STRAIGHT OBJECTIVE TYPE QUESTIONS)
6 Videos
- VISCOSITY BOOK - AAKASH SERIESCHAPTER - VISCOSITY EXERCISE - Questions for Descriptive Answers
3 Videos
- WORK POWER ENERGYBOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 3
61 Videos
Similar Questions
A particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .
.
View SolutionA particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .
.
View Solution
Knowledge Check
A particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .A3sinθ=2cosθ'B2sinθ=3cosθ'C3sinθ'=2cosθD2sinθ=3cosθ'
.A3sinθ=2cosθ'B2sinθ=3cosθ'C3sinθ'=2cosθD2sinθ=3cosθ'A practical moves from rest at A on the surface of a smooth circular cylinder of radius r as shown . At B it leaves the cylinder. The equation relating αandβ is
 A3sinα=2sinβB2sinα=3cosβC3sinβ=2cosαD2sinβ=3cosα
A3sinα=2sinβB2sinα=3cosβC3sinβ=2cosαD2sinβ=3cosαA particle of mass m is going along surface of smooth hemisphere of radius R in verticle plane. At the moment shown its speed is v. Choose correct option(s).
 Amg−Ncosθ=m(gsin2θ−v2Rcosθ)BN−mgcosθ=mv2RCmg−Nsinθ=mv2RDNsinθ=m(gsinθcosθ−v2Rsinθ)
Amg−Ncosθ=m(gsin2θ−v2Rcosθ)BN−mgcosθ=mv2RCmg−Nsinθ=mv2RDNsinθ=m(gsinθcosθ−v2Rsinθ)
A partical moves from rest at A on the surface of a smooth circule cylinder of radius r as shown . At B it leavels the cylinder. The equation releaseder . The equation relating αandβ is

View SolutionA particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View SolutionA small block of mass m has speed√gR2 at the top most point of a fixed hemisphere of radius R as shown in figure. The angle θ, when block loses the contact with the hemisphere is
_PHY_E05_149_Q01.png)
View SolutionA particle of mass m is placed in equlibrium at the top of a fixed rough hemisphere of radius R. Now the particle leaves the contact with the surface of the hemisphere at angular position θ with the vertical wheere cosθ35. if the work done against frictiion is 2mgR10x, find x.
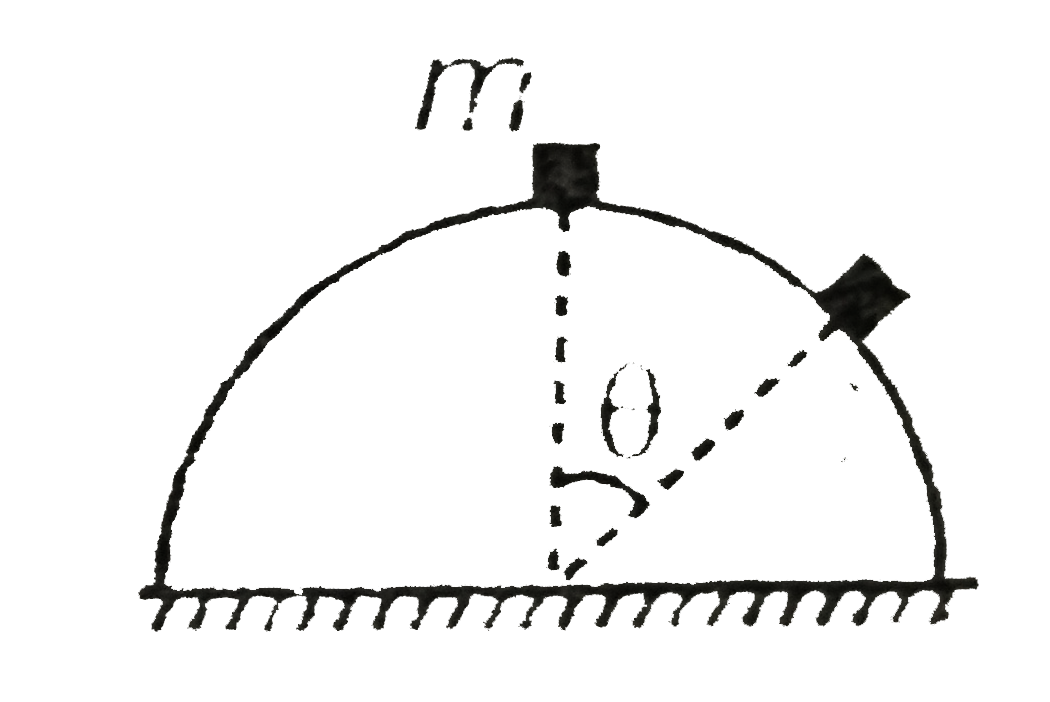
View SolutionA particle of mass m is placed in equilibrium at the top of a fixed rough hemisphere of radius R. Now the particle leaves the contact with the surface of the hemisphere at angular position θ with the vertical where cosθ=35. if the work done against friction is 2mgR10x, find x.
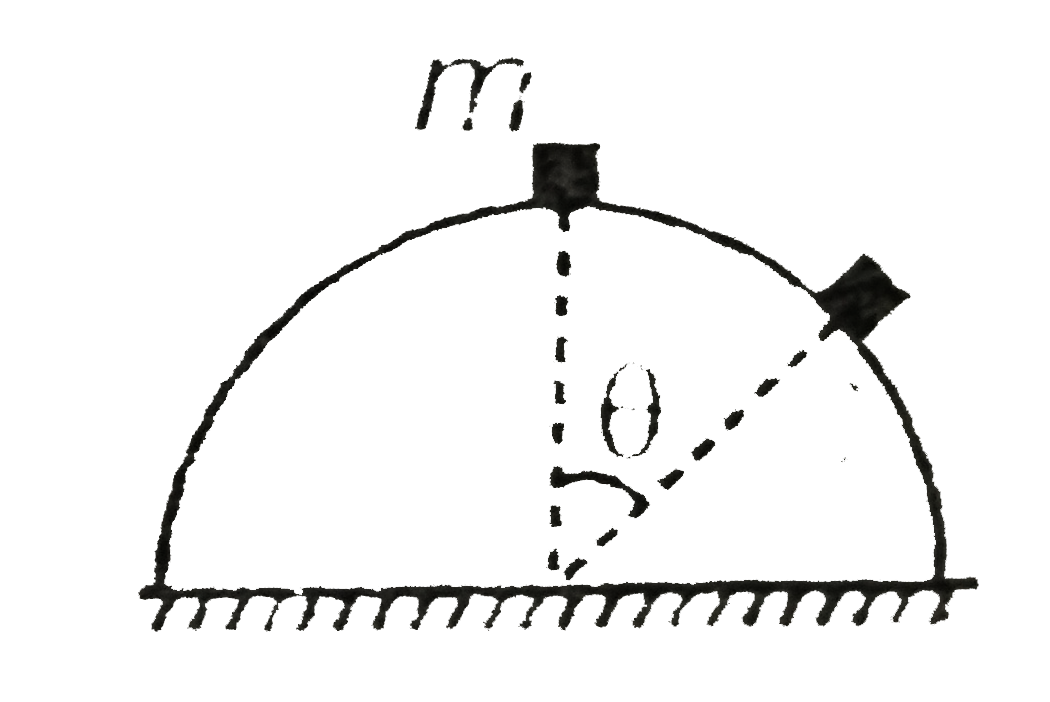
View Solution
