A particle of mass m is placed in equilibrium at the top of a fixed rough hemisphere of radius R. Now the particle leaves the contact with the surface of the hemisphere at angular position θ with the vertical where cosθ=35. if the work done against friction is 2mgR10x, find x.
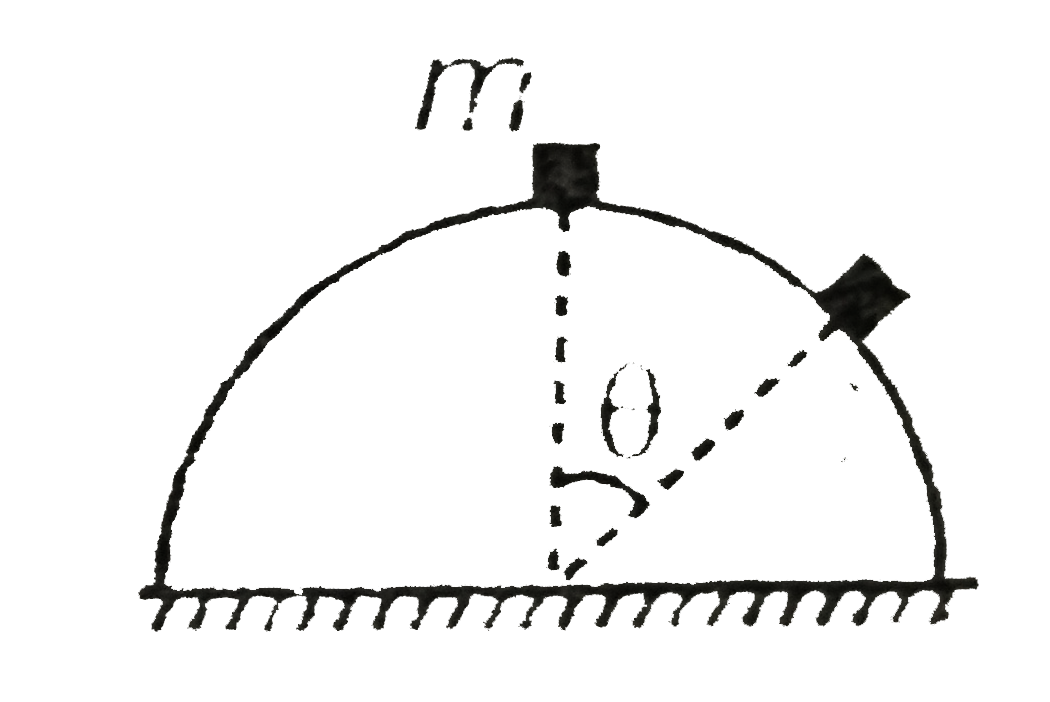
The correct Answer is:2
Step by step video & image solution for A particle of mass m is placed in equilibrium at the top of a fixed rough hemisphere of radius R. Now the particle leaves the contact with the surface of the hemisphere at angular position theta with the vertical where cos theta"="(3)/(5). if the work done against friction is (2mgR)/(10x), find x. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-H (MULTIPLE TRUE FALSE TYPE QUESTIONS)
10 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-I (SUBJECTIVE TYPE QUESTIONS)
6 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-F (MATRIX-MATCH TYPE QUESTIONS)
5 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A small block of mass m has speed√gR2 at the top most point of a fixed hemisphere of radius R as shown in figure. The angle θ, when block loses the contact with the hemisphere is
_PHY_E05_149_Q01.png)
View SolutionA particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .
.
View SolutionA particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .
.
View SolutionA block of mass m moving on a fixed smooth hemisphere of rudius R. If speed of block at top most point of the hemisohere is √gR as shown in the figure, then the angle (θ) with the vertical, where the normal contact force becomes zero will be
View SolutionA particle rests on the top of a smooth hemisphere of radius r. It is imparted a horizontal velocity of √ηgr. Find the angle made by the radius vector joining the particle with the vertical at the instant the particle losses contact with the sphere.

View SolutionA small particle is placed at the top point A of a fixed smooth hemisphere of radius R. Particle is given small displacement towards right and it starts slipping. Calculate velocity of the particle after hitting horizontal perfectly inelastic surface.
View SolutionA particle of mass m is projected with speed √Rg4 from top of a smooth hemisphere as shown in figure. If the particle starts slipping from the highest point, then the horizontal distance between the point where it leaves contact with sphere and the point at which the body was placed is
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionA particle of mass m is kept on a fixed, smooth sphere of radius R at a position, where the radius through the particle makes an angle of 30 ∘ with the vertical. The particle is released from this position. (a) What is the force exerted by the sphere on the particle just after the release? (b) Find the distance traveled by the particle before it leaves contact with the sphere.
View SolutionA particle of mass m is released in a smooth hemispherical bowl from shown position A. Find work done by gravity as it reaches the lowest point B.
View Solution
