A particle slides down from rest on an inclined planet of angle θ with horizontal and the distances are as shown. The particle slides down from top to the position A, where it's velocity is v. Then below correct options are

(V2−2gH) will remain constant
(V2−2gSsinθ) will remain constant
[V2−2gSH−hp−s] will remain constant
[V2−2gSHp] will remain constant
The correct Answer is:A, B, C, D
Topper's Solved these Questions
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET ADVANCED LINKED COMPREHENSION TYPE QUESTIONS)
5 Videos
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET ADVANCED MATRIX MATCHING TYPE QUESTIONS)
1 Videos
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET ADVANCED STRAIGHT OBJECTIVE TYPE QUESTIONS)
3 Videos
- VISCOSITY BOOK - AAKASH SERIESCHAPTER - VISCOSITY EXERCISE - Questions for Descriptive Answers
3 Videos
- WORK POWER ENERGYBOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 3
61 Videos
Similar Questions
A block slides down an inclined plane that makes an angle θ with the horizontal. If the coefficient of kinetic friction is μ, find the acceleration of the block.
View SolutionA trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.

View Solution
Knowledge Check
A particle sides down from rest on an inclined plane of angle θ with horizontal. The distances are as shown. The particle slides down to the position A, where it velocity is v.
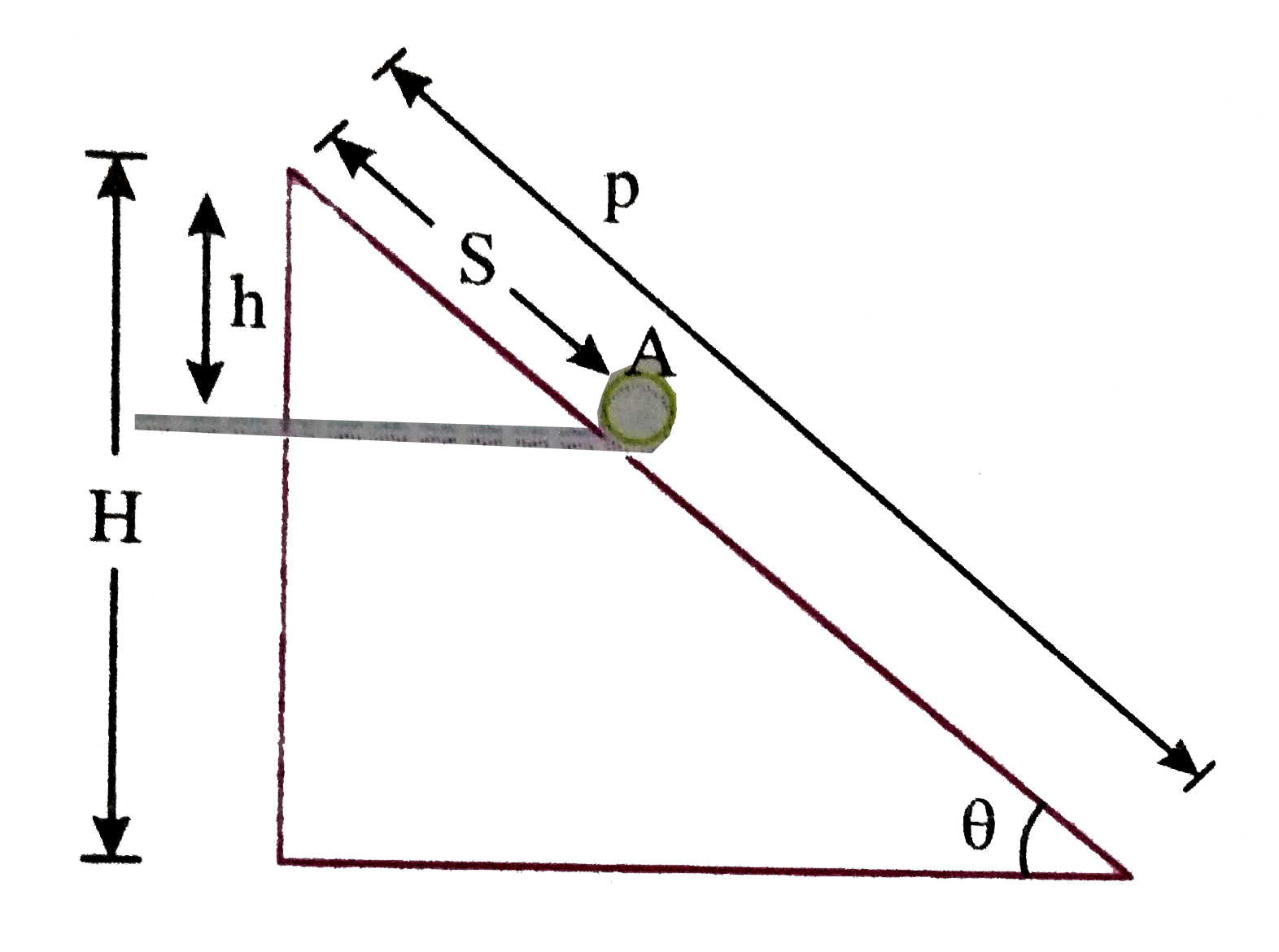 .A(v2−2gh) will remain zeroB(v2−2gssinθ) will remain zeroC[v2−2gs(H−h)(p−s)] will remain zeroD[v2−2gsHp] will remain zero.
.A(v2−2gh) will remain zeroB(v2−2gssinθ) will remain zeroC[v2−2gs(H−h)(p−s)] will remain zeroD[v2−2gsHp] will remain zero.A block is released from the top of an inclined plane of inclination θ. Its velocity at the bottom of plane is v. If it slides down a rough inclined plane of the same inclination , its velocity at bottom is v/2. The coefficient of friction is
A34cosθB14cosθC14tanθD34tanθA trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.
 Aθ=α2Bθ=2αCθ=zeroDθ=α
Aθ=α2Bθ=2αCθ=zeroDθ=α
A particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle of mass m is released from rest from a point A of a wedge of mass 4m free to slide on a frictionless horizontal plane.The particle slides down the smooth face AB of the wedge.When the velocity of the wedge is 0.2m/s the velocity of the particle in m/s relative to the wedge is
View SolutionA smooth inclined plane is inclined at an angle θ with the horizontal. A body starts from rest and slides down the inclined surface. The time taken by the body to reach the bottom is
View Solution
