In the arrangement shwon, initially both springs are in their natural length l0. The left spring has force constnat k0=2N/m and the force constant of the right spring varies as k=k0x, where x is its compression. The mass of the block is 10/3 kg. At time t=0, the block is given a right ward velocity v0=2 m/s. Both the springs are massless.

When the block has moved through distance x0 m to the right, the elastic potential energy stored in the right spring is
2x303J
x202J
x306J
43x30J
The correct Answer is:A
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET ADVANCED MATRIX MATCHING TYPE QUESTIONS)1videos
WORK -POWER-ENERGY
- BOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET ADVANCED INTEGER TYPE QUESTIONS)10videos
WORK -POWER-ENERGY
- BOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET ADVANCED MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)2videos
WORK -POWER-ENERGY
- BOOK - AAKASH SERIESCHAPTER - VISCOSITY EXERCISE - Questions for Descriptive Answers3videos
VISCOSITY
- BOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 361videos
WORK POWER ENERGY
Similar Questions
Block of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.
 View Solution
View SolutionAs shown in the figure, initially both th springs are in normal length (L0). At t=0, the block is given a rightward velocity v0=2m/s. The mass of the block is (14/3)kg. How much distance does th block cover before it comes to rest for the first time? (The spring constant of the left spring is K0=2N/m and that of the right spring is not constant and varies as k=k0x, where x is the compression in the spring)
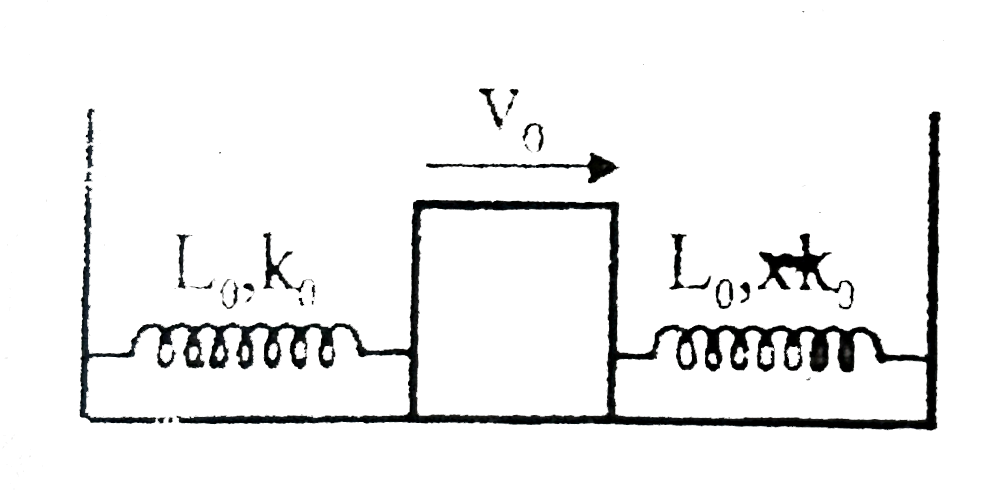 View Solution
View Solution
Knowledge Check
- Question 1 - Select One

A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2 - Question 2 - Select One
As shown in the figure, initially both th springs are in normal length (L0). At t=0, the block is given a rightward velocity v0=2m/s. The mass of the block is (14/3)kg. How much distance does th block cover before it comes to rest for the first time? (The spring constant of the left spring is K0=2N/m and that of the right spring is not constant and varies as k=k0x, where x is the compression in the spring)
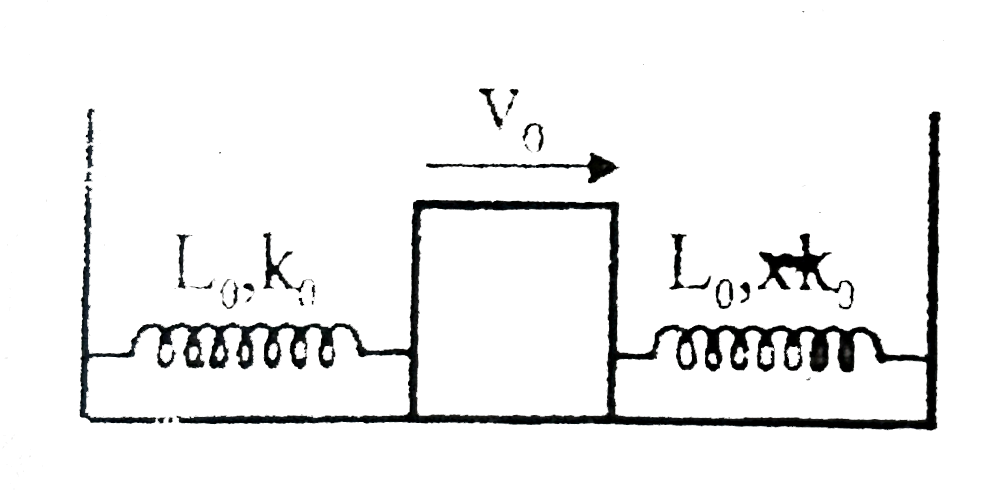 A2mB4mC6mD8m
A2mB4mC6mD8m - Question 3 - Select One
A block of mass 2kg is connected with a spring of natural length 40cm of force constant K=200N/m. The cofficient of friction is μ=0.5. When released from the given position, acceleration of block will be
 AzeroB2m/s2C6m/s2D8m/s2
AzeroB2m/s2C6m/s2D8m/s2
A block of mass 2kg is connected with a spring of natural length 40cm of force constant K=200N/m. The cofficient of friction is μ=0.5. When released from the given position, acceleration of block will be
 View Solution
View SolutionA 700 g block is released from rest at height h0 above a vertical spring with spring constant k=450N/m and negligible mass. The block sticks to the spring and momentarily stops after compressing the spring 19.0 cm. How much work is done (a) by the block on the spring and (b) by the spring on the block ? (c) What is the value of h0 ? (d) If the block were released from height 2.00h0 above the spring, what would be the maximum compression of the spring ?
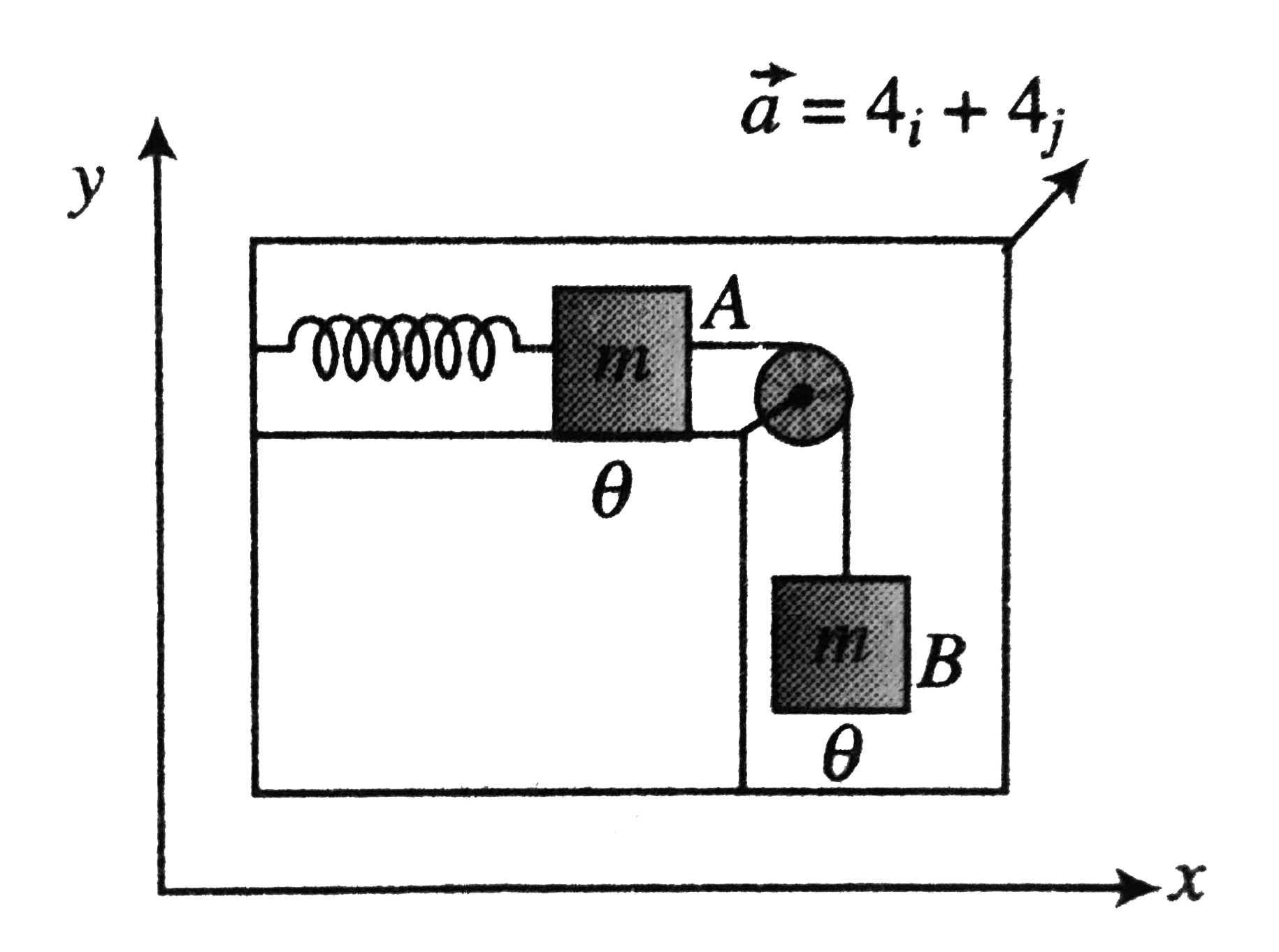
View SolutionThe arrangement shown in figure is at rest. An ideal spring of natural length l0 having spring constant k=220Nm−1, is connected to block A. Blocks A and B are connected by an ideal string passing through a friction less pulley. The mass of each block A and B is equal to m=2kg when the spring was in natural length, the whole system is given an acceleration →a as shown. If coefficient of friction of both surfaces is μ=0.25, then find the maximum extension in 10(m) of the spring. (g=10ms−2).
 View Solution
View SolutionThe arrangement shown in figure is at rest. An ideal spring of natural length l0 having spring constant k=220Nm−1, is connected to block A. Blocks A and B are connected by an ideal string passing through a frictionless pulley. The mass of each block A and B is equal to m=2kg when the spring was in natural length, the whole system is given an acceleration →a as shown. If coefficient of friction of both surfaces is μ=0.25, then find the maximum extension in (cm) of the spring. (g=10ms−2).
 View Solution
View SolutionA block of mass m is placed on a smooth block of mass M=m with the help of a spring as shown in the figure. A velocity v0 is given to upper block when spring is in natural length. Find maximum compression in the spring.
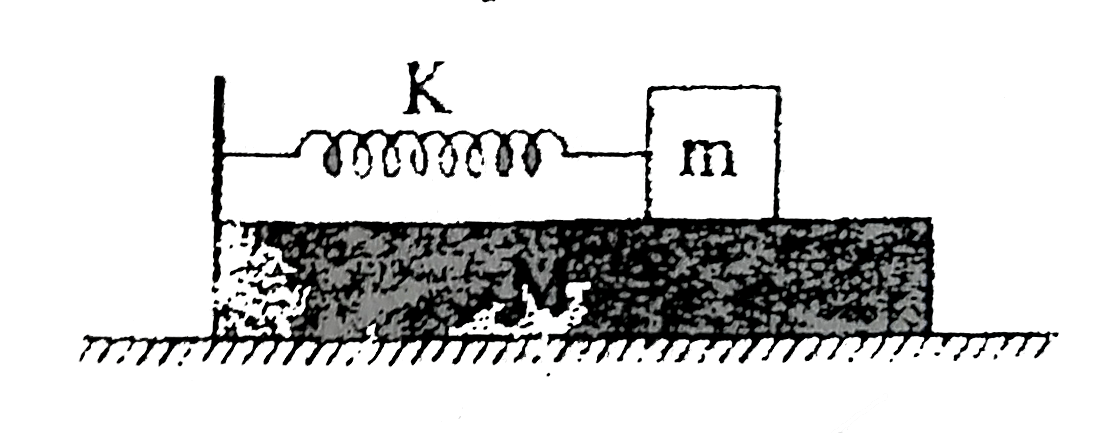 View Solution
View Solution

