In the arrangement shwon, initially both springs are in their natural length l0. The left spring has force constnat k0=2N/m and the force constant of the right spring varies as k=k0x, where x is its compression. The mass of the block is 10/3 kg. At time t=0, the block is given a right ward velocity v0=2 m/s. Both the springs are massless.

When the blcok comes to instantaneous rest th energy stored in the left spring is
3J
12.25 J
6.25 J
16 J
The correct Answer is:A
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET ADVANCED MATRIX MATCHING TYPE QUESTIONS)1videos
WORK -POWER-ENERGY
- BOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET ADVANCED INTEGER TYPE QUESTIONS)10videos
WORK -POWER-ENERGY
- BOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET ADVANCED MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)2videos
WORK -POWER-ENERGY
- BOOK - AAKASH SERIESCHAPTER - VISCOSITY EXERCISE - Questions for Descriptive Answers3videos
VISCOSITY
- BOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 361videos
WORK POWER ENERGY
Similar Questions
Block of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.
 View Solution
View SolutionIn the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
A0.01 mB0.1mC0.2 mD0.5 m - Question 2 - Select One
A body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
A0.01 mB0.1 mC0.2 mD0.5 m - Question 3 - Select One
As shown in the figure, initially both th springs are in normal length (L0). At t=0, the block is given a rightward velocity v0=2m/s. The mass of the block is (14/3)kg. How much distance does th block cover before it comes to rest for the first time? (The spring constant of the left spring is K0=2N/m and that of the right spring is not constant and varies as k=k0x, where x is the compression in the spring)
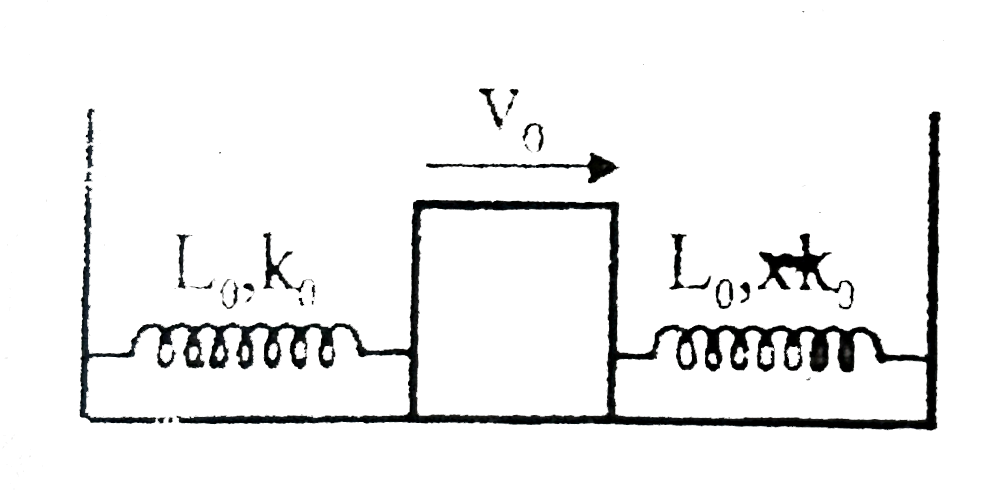 A2mB4mC6mD8m
A2mB4mC6mD8m
In the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.
 View Solution
View SolutionA body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
View SolutionAs shown in the figure, initially both th springs are in normal length (L0). At t=0, the block is given a rightward velocity v0=2m/s. The mass of the block is (14/3)kg. How much distance does th block cover before it comes to rest for the first time? (The spring constant of the left spring is K0=2N/m and that of the right spring is not constant and varies as k=k0x, where x is the compression in the spring)
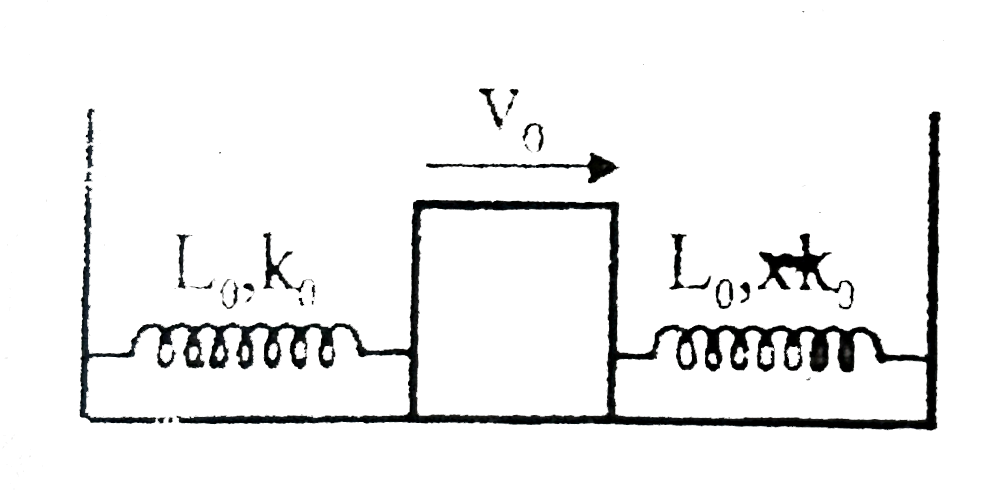 View Solution
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is
 View Solution
View Solution
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenView Solution

