In the figure a and b AC, DG and GF ar fixed inclined planes BC=EF=x and AB=DE=y. A small block of mass m is released from the point A. It slides down AC and reaches C with speed VC. The same block is released from rest from the point D, It slides down DGF and reaches the point F with speed VF, Coefficient of kinetic frictions between the block and bot the surfaces AC and DGF are μ. The values of VC and VF is √kgy−μgx then find the value of k.

The correct Answer is:2
Topper's Solved these Questions
- WORK -POWER-ENERGYBOOK - AAKASH SERIESCHAPTER - WORK -POWER-ENERGYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET ADVANCED INTEGER TYPE QUESTIONS)
10 Videos
- VISCOSITY BOOK - AAKASH SERIESCHAPTER - VISCOSITY EXERCISE - Questions for Descriptive Answers
3 Videos
- WORK POWER ENERGYBOOK - AAKASH SERIESCHAPTER - WORK POWER ENERGYEXERCISE - EXERCISE - 3
61 Videos
Similar Questions
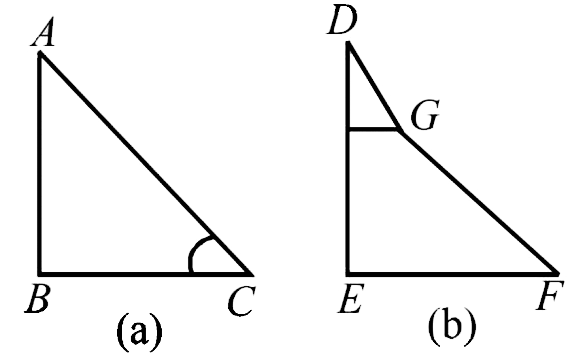
In the figure (a) and (b) AC and GF are fixed inclined planes BC=EF=x and AB=DE=y A small block of mass M is rdeased from the point A it sides down AC and maches C with a speed VC The same block is relessed from rest from the point D it sides down DGF and reached the point the F with VpTHecoefficientsofki≤ticictionbetweentheblockandthesarfaceACandDGFaremucolca––teV_(C) andV(p)
View SolutionA block is released from rest from point on a rough inclined place of inclination 37∘. The coefficient of friction is 0.5.
View Solution
Knowledge Check
Block A of mass M in the system shown in the figure slides down the incline at a constant speed. The coefficient of friction between block A and the surface is 1 3 3 . The mass of block B is-
 Am/2Bm/3C2m/3Dm/√3
Am/2Bm/3C2m/3Dm/√3A block is released from rest from point on a rough inclined place of inclination 37∘. The coefficient of friction is 0.5.
AThe time taken to slide down 9 m on the plane is 3 s.BThe velocity of block after moving 4 m is m/s.CThe block travels equal distances in equal intervals of time.DThe velocity of block increases linearly.A block of mass m released from rest from point O as shown below. The velocity of the block at the lowest points are v O , v E, v F respectively. Assume coefficient of kinetic friction between surface and the block is same in all cases. Then,
(a) AvD>vE>vFBvf>vE>vDCvD=vE=vFDvD=vEvF=0
AvD>vE>vFBvf>vE>vDCvD=vE=vFDvD=vEvF=0
A block slides down a curved frictionless track and then up an inclined plane as in figure. The coefficient of kinetic friction between the block and incline is μk. Find the maximum height reached by the block.

View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is .
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block has been placed on an inclined plane . The slope angle of θ of the plane is such that the block slides down the plane at a constant speed . The coefficient of kinetic friction is equal to :
View Solution
