Find the are length of the cardioid ρ=a(1+cosφ)(a>0,0≤φ≤2π)
The correct Answer is:8a
Topper's Solved these Questions
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Area of Surface of Revolution
10 Videos
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Geometrical Applications of the Definite Integral
10 Videos
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - The Arc Length of a Curve Represented Parametrically
4 Videos
- APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSBOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - ADDITIONAL PROBLEMS
9 Videos
- BASIC CLASSES OF INTEGRABLE FUNCTIONS BOOK - IA MARONCHAPTER - BASIC CLASSES OF INTEGRABLE FUNCTIONS EXERCISE - 5.8 INTEGRATION OF OTHER TRANSCENDENTAL FUNCTIONS
5 Videos
Similar Questions
Find the Cartesian coordinates of the center of gravity of the are of the cardioid ρ=a(1+cosφ) between φ=0andφ=π.
View SolutionFind the length of the closed curve ρ=asin4φ4
View SolutionComputes the area of the surface formed by revolving one branch of the lemniscate ρ=a√cos2φ about the straight line φ=π4
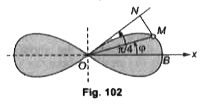
View SolutionCompute the volume of the solid obtained by revolving about the polar axis the cardioid ρ=a(1+cosφ) shown in
View SolutionFind the length of the lemniscate ρ2=2a2cos2φ between the right-hand vertex corresponding to φ=0 and any point with a polar angle φ<π4
View SolutionFind the area of the regions bounded by the curve ρ=2acos3φ and the arcs of the circle ρ=a and situated outside the circle.
View SolutionCompute the length of the segment of the straight line ρ=asec(φ−π3) between φ=0andφ=π2
View SolutionFind the length of the logarithmic spiral ρ=aemϕ between a certain point (ρ0,φ0) and a moving point (ρ,φ)
View SolutionCompute the area of the figure bounded by the circle ρ=3√2acosφandρ=3asinφ
View SolutionFind the length of the first turn of the spiral of the Archimedes ρ=aφ
View Solution
