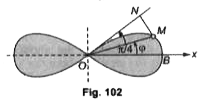
Compute the volume of the solid obtained by revolving about the polar axis the cardioid ρ=a(1+cosφ) shown in
The correct Answer is:830πa3(u=cosφ)
Topper's Solved these Questions
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - The Arc Length of a Plane Curve in Rectangular Coordinates
7 Videos
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - The Arc Length of a Curve Represented Parametrically
4 Videos
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - The Area of a Curvilinear Sector in Polar Coordinates
5 Videos
- APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSBOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - ADDITIONAL PROBLEMS
9 Videos
- BASIC CLASSES OF INTEGRABLE FUNCTIONS BOOK - IA MARONCHAPTER - BASIC CLASSES OF INTEGRABLE FUNCTIONS EXERCISE - 5.8 INTEGRATION OF OTHER TRANSCENDENTAL FUNCTIONS
5 Videos
Similar Questions
Compute the volume of the solid generated by revolving about the x-axis the area bounded by the axes of coordinates and the parabola x12+y12=a12.
View SolutionCompute the volume of the solid generated by revolving about the y-axis the figure bounded by the parabolas y=x2and8x=y2
View SolutionCompute the volume of the solid generated by revolving about the x-axis the figure bounded by the parabola y=0.25x2+2 and the straight line 5x−8y+14=0
View SolutionFind the volume of the solid generated by revolving about the x-axis the figure enclosed by the astroid : x=acos3t,y=asin3t.
View SolutionCompute the area of the surface formed by revolving the lemniscate ρ=a√cos2φ about the polar axis.
View SolutionFind the Cartesian coordinates of the center of gravity of the are of the cardioid ρ=a(1+cosφ) between φ=0andφ=π.
View SolutionFind the are length of the cardioid ρ=a(1+cosφ)(a>0,0≤φ≤2π)
View SolutionFind the volume of the solid generated by revolving about the x-axis the figure bounded by the straight lines y=x+1,y=2x+1andx=2.
View SolutionComputes the area of the surface formed by revolving one branch of the lemniscate ρ=a√cos2φ about the straight line φ=π4
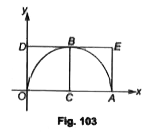
View SolutionGiven: the cycloid x=a(t−sint),y=a(1−cost),0≤t≤2π
Compute. (a) the areas of the surface formed by revolving the arc OBA about the x and y-axis,
(b) the volumes of the solids generated by revolving the figure OBAO about the y-axis and the axis BC,
(c ) the area of the surface generated by revolving the are BA about the axis BC,
(d) the volume of the solid generated by revolving the figure ODBEABO about the tangent line DE touching the figure at the vertex B,
(e ) the area of the surface formed by revolving the are of the cycloid (see item (d)]
View Solution
