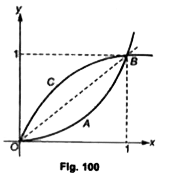
Find the area of the surface generated by revolving about the x-axis a closed contour OABCO formed by the curves y=x2andx=y2
The correct Answer is:67√5π48−π32ln(2+√5)−π6
Topper's Solved these Questions
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Geometrical Applications of the Definite Integral
10 Videos
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - Computing Pressure, Work and Other Physical Quantities by the Definite Integrals
7 Videos
- APPLICATIONS OF THE DEFINITE INTEGRALBOOK - IA MARONCHAPTER - APPLICATIONS OF THE DEFINITE INTEGRALEXERCISE - The Arc Length of a Curve in Polar Coordinates
7 Videos
- APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSBOOK - IA MARONCHAPTER - APPLICATION OF DIFFERENTIAL CALCULUS TO INVESTIGATION OF FUNCTIONSEXERCISE - ADDITIONAL PROBLEMS
9 Videos
- BASIC CLASSES OF INTEGRABLE FUNCTIONS BOOK - IA MARONCHAPTER - BASIC CLASSES OF INTEGRABLE FUNCTIONS EXERCISE - 5.8 INTEGRATION OF OTHER TRANSCENDENTAL FUNCTIONS
5 Videos
Similar Questions
Compute the volume of the solid generated by revolving about the y-axis the figure bounded by the parabolas y=x2and8x=y2
View SolutionCompute the area of the a surface generated by revolving about the x-axis an are of the curve x=t2,y=t3(t2−3) between the points of intersection of the curve and the x-axis
View Solution
Knowledge Check
The volume of solid generated by revolving about the y-axis the figure bounded by the parabola y=x2andx=y2 is
A215πB245πC215πD524πArea bounded by the curve y=x2+x−6 and the X-axis is
A1276B2256C1256DNone of these
Find the volume of the solid generated by revolving about the x-axis the figure bounded by the straight lines y=x+1,y=2x+1andx=2.
View SolutionFind the area between the curves y=x2 and x=y2.
View SolutionFind the volume of the solid generated by revolving, about the x-axis, the infinite branch of the curve y=2(1x−1x2)forx≥1.
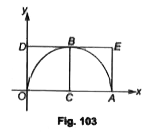
View SolutionGiven: the cycloid x=a(t−sint),y=a(1−cost),0≤t≤2π
Compute. (a) the areas of the surface formed by revolving the arc OBA about the x and y-axis,
(b) the volumes of the solids generated by revolving the figure OBAO about the y-axis and the axis BC,
(c ) the area of the surface generated by revolving the are BA about the axis BC,
(d) the volume of the solid generated by revolving the figure ODBEABO about the tangent line DE touching the figure at the vertex B,
(e ) the area of the surface formed by revolving the are of the cycloid (see item (d)]
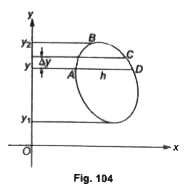
View SolutionProve that if the figure S is bounded by a simple convex contour and is situated between the ordinates y1andy2, then the volume of the solid generated by revolving this figure about the x-axis can be expressed by the formula
V=2π∫y2y1yhdy,
where h=x2(y)−x1(y),x=x1(y) being the equation of the left portion of the contour and x=x2(y) that of the right portion.
View SolutionFind the area of the surface obtained by revolving a loop of the curve 9ax2=y(3a−y)2 about the y-axis
View Solution
