Find the volume of the solid generated by revolving, about the x-axis, the infinite branch of the curve .
The correct Answer is:
Topper's Solved these Questions
- IMPROPER INTEGRALSBOOK - IA MARONCHAPTER - IMPROPER INTEGRALSEXERCISE - 8.4 ADDITIONAL PROBLEMS
1 Videos
- IMPROPER INTEGRALSBOOK - IA MARONCHAPTER - IMPROPER INTEGRALSEXERCISE - 8.2 IMPROPER INTEGRALS OF UNBOUNDED FUNCTIONS
5 Videos
- DIFFERENTIATION OF FUNCTIONS BOOK - IA MARONCHAPTER - DIFFERENTIATION OF FUNCTIONS EXERCISE - 2.7 (ADDITIONAL PROBLEMS)
7 Videos
- INDEFINITE INTEGRALS, BASIC METHODS OF INTEGRATIONBOOK - IA MARONCHAPTER - INDEFINITE INTEGRALS, BASIC METHODS OF INTEGRATIONEXERCISE - 4.4. Reduction Formulas
2 Videos
Similar Questions
Knowledge Check
The volume of solid generated by revolving about the y-axis the figure bounded by the parabola y=x2andx=y2 is
A215πB245πC215πD524π
Find the volume of the solid generated by revolving about the x-axis the figure enclosed by the astroid : x=acos3t,y=asin3t.
View SolutionCompute the volume of the solid generated by revolving about the x-axis the area bounded by the axes of coordinates and the parabola x12+y12=a12.
View SolutionCompute the volume of the solid generated by revolving about the x-axis the figure bounded by the parabola y=0.25x2+2 and the straight line 5x−8y+14=0
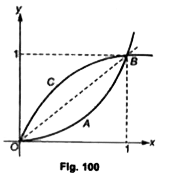
View SolutionFind the area of the surface generated by revolving about the x-axis a closed contour OABCO formed by the curves y=x2andx=y2
View SolutionFind the volume of the solid generated by revolving about the line y=−2a the figure bounded by the parabola y2=4ax and the straight line x=a

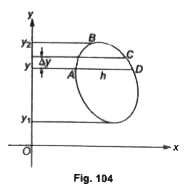
View SolutionProve that if the figure S is bounded by a simple convex contour and is situated between the ordinates y1andy2, then the volume of the solid generated by revolving this figure about the x-axis can be expressed by the formula
V=2π∫y2y1yhdy,
where h=x2(y)−x1(y),x=x1(y) being the equation of the left portion of the contour and x=x2(y) that of the right portion.
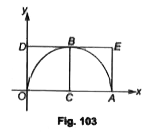
View SolutionGiven: the cycloid x=a(t−sint),y=a(1−cost),0≤t≤2π
Compute. (a) the areas of the surface formed by revolving the arc OBA about the x and y-axis,
(b) the volumes of the solids generated by revolving the figure OBAO about the y-axis and the axis BC,
(c ) the area of the surface generated by revolving the are BA about the axis BC,
(d) the volume of the solid generated by revolving the figure ODBEABO about the tangent line DE touching the figure at the vertex B,
(e ) the area of the surface formed by revolving the are of the cycloid (see item (d)]
View Solution
