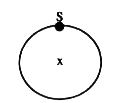
A ring is suspended from a points S on its rim as shwon in the fitgure. When diplaced from equilibrium, it oscillates with the period of 2 seconds. The radius of the ring is (take g=π2)
 Solution in Telugu
Solution in Telugu
0.5 m
0.5 m
0.15 m
1.0 m
The correct Answer is:B
Step by step video & image solution for A ring is suspended from a points S on its rim as shwon in the fitgure. When diplaced from equilibrium, it oscillates with the period of 2 seconds. The radius of the ring is (take g=pi^(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE-3
49 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - PROBLEM
249 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE-1B
20 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
Similar Questions
The displacement of two particles executing S.H.M are represented by y1=asin(wt+ϕ) and y2=acoswt. The phase difference between the velocities of these particles is
View SolutionWhich of the following examples represent simple harmonic motion and which represent periodic but not simple harmonic motion?
View Solution(A) : All oscillatory motions are necessarily periodic motion in conservative fields but all periodic motion are not oscillatory.
(R) : Simple pendulum is an example of oscillatory motion.
View SolutionThe spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find the amplitude and the time period of the motion of the block.

View SolutionWhat is Physics ?
View SolutionA ring of radius r is suspended from a point on its circumference. Determine its angular frequency of small oscillations.

View SolutionA seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of 4 m//s^(2) . Its period of oscillation is
View SolutionA uniform ring of radius 'R' is suspended from a horizontal nail 'A' as shown. Find time period of its small oscillations.
View SolutionWhen a mass M is suspended from a spring, its period of oscillation is 2 second. If a mass 4 M is suspended from the same spring, then its period of oscillation will be
View SolutionA ring is suspended at a point on its rim and it behaves as a second's pendulum when it oscillates such that its centre move in its own plane. The radius of the ring would be (g = pi^(2))
View SolutionA ring is suspended at a point on its rim and it behaves as a second’s pendulum when it oscillates such that its centre move in its own plane. The radius of the ring would be (g = π2)
View SolutionA ring is oscillating about a horizontal axis passes through its rim. Determine time period of oscillation.
View SolutionA ring of the radius r is suspended from a point on its circumference. If the ring is made to oscillate in the plane of the figure, then the angular frequency of these small oscillations is
View SolutionA uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
View SolutionA particle suspended from a vertical spring oscillates 10 times per second. At the highest point of oscillation, the spring becomes unstretched. Take g=π2m⋅s−2
The maximum speed of the particle is
View SolutionA ring is suspended from a points S on its rim as shwon in the fitgure. When diplaced from equilibrium, it oscillates with the period of 2 seconds. The radius of the ring is (take g=π2)

View Solution
