A conical vessel without a bottom tightly stands on a table. A liquid is poured into the vessel and as soon as its level reaches a height h. The pressure the liquid raises the vessel. The radius of the bottom greater base of the vessel is R, the semi- vertex angel of the cone is, ∝ and the weight of the vessel is W. What is the density of the liquid ?
Wπgh2tan2∝(R+13htan∝)
Wπgh2tan∝(R+13htan∝)
Wπgh2tan∝(R−htan∝3htan∝)
Wπgh2tan∝(R−13tan∝)
The correct Answer is:D
Topper's Solved these Questions
- FLUID MECHANICSBOOK - AAKASH SERIESCHAPTER - FLUID MECHANICSEXERCISE - Problems
60 Videos
- FLUID MECHANICSBOOK - AAKASH SERIESCHAPTER - FLUID MECHANICSEXERCISE - Test your self
6 Videos
- FLUID MECHANICSBOOK - AAKASH SERIESCHAPTER - FLUID MECHANICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II (Linked Comprehension Type Questions Passage: III)
3 Videos
- EXPANSION OF SOLIDS BOOK - AAKASH SERIESCHAPTER - EXPANSION OF SOLIDS EXERCISE - Questions for Descriptive Answers
5 Videos
- FRICTION BOOK - AAKASH SERIESCHAPTER - FRICTION EXERCISE - ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANCED) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
1 Videos
Similar Questions
A conical vessel wihout a bottom stands on a table. A liquid is poured with the vessel & as soon as the level reaches h, the pressure of the liquid raises the vessel. The radius of the base of the vessel is R and half angle of the cone α and the weight of the vessel is W. What is the density of the liquid ?

View SolutionA conical vessel wihout a bottom stands on a table. A liquid is poured with the vessel & as soon as the level reaches h, the pressure of the liquid raises the vessel. The radius of the base of the vessel is R and half angle of the cone α and the weight of the vessel is W. What is the density of the liquid ?

View Solution
Knowledge Check
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
A8cmB2cmC40cmD4cmTwo vessels A and B of cross sections as shown contain a liquid up to the same height. As the temperature rises, the liquid pressure at the bottom (neglecting expansion of the vessels ) will :
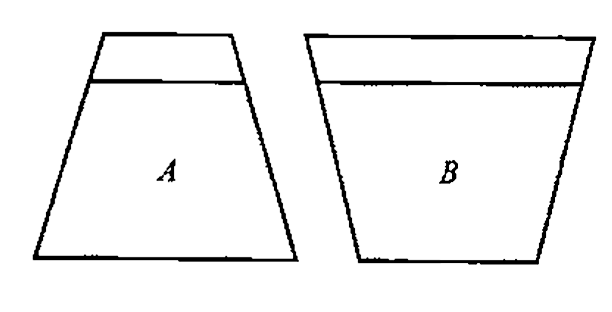 AIncrease in A , decrease in BBincrease in B , decrease in ACIncrease in both A and B but more in ADIncrease in both A and B equally
AIncrease in A , decrease in BBincrease in B , decrease in ACIncrease in both A and B but more in ADIncrease in both A and B equallyA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
Ah=2π2n2r2gBh=4π2n2r2gCh=π2r2n2gDh=π2r2n2g
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
View SolutionA liquid has been poured into a cylindrical vessel. What shape will the surface of the liquid have if the vessel is rotated uniformly about its axis with an angular velocity ω ?
View SolutionThe three vessels shown in figure have same base area. Equal volumes of a liquid are poured in three vessels. The force on the base will be
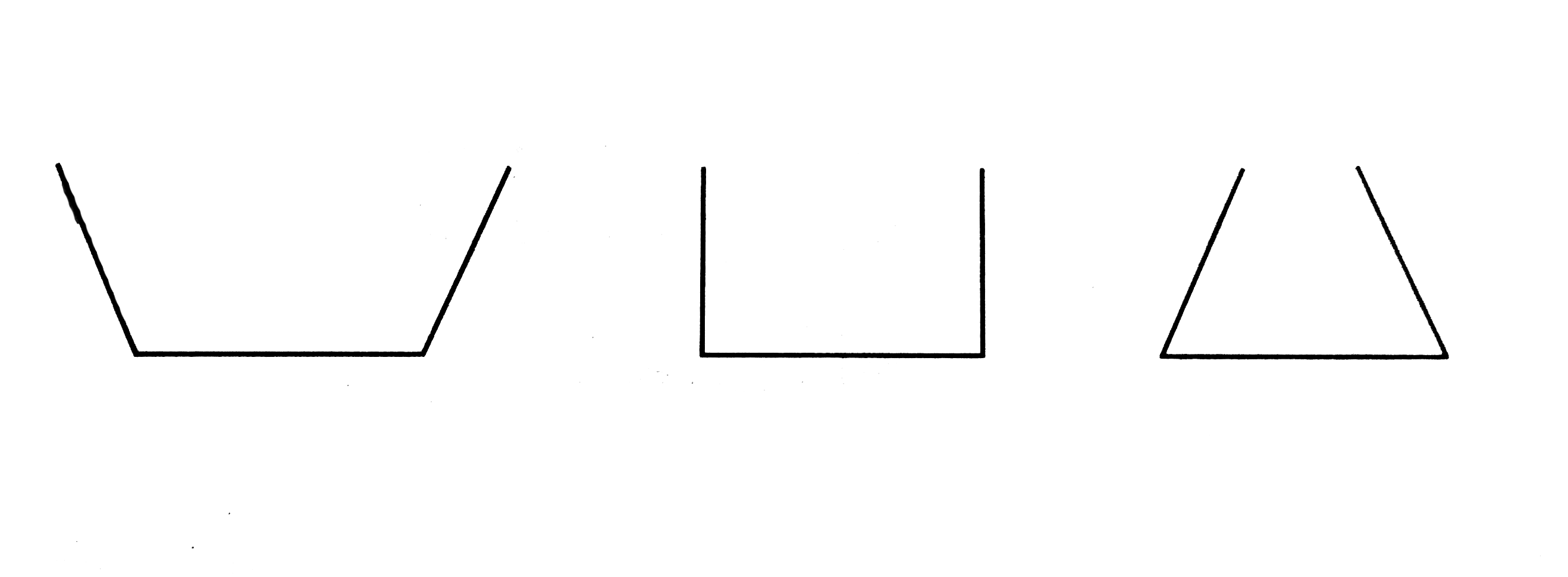
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
View Solution
