A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
8cm
2cm
40cm
4cm
The correct Answer is:A
To solve the problem of the height difference of the liquid in a rotating cylindrical vessel, we can follow these steps:
Step 1: Understand the Problem
We have a cylindrical vessel with a radius of r=5cm=0.05m that is rotating at n=4rev/s. We need to find the difference in height h between the center and the sides of the liquid in the vessel.
Step 2: Convert Revolutions per Second to Angular Velocity
The angular velocity ω in radians per second can be calculated using the formula:
ω=2πn
Substituting the given value:
ω=2π×4=8πrad/s
Step 3: Calculate the Linear Velocity
The linear velocity v at the radius r can be calculated using the formula:
v=ωr
Substituting the values:
v=(8π)×(0.05)=0.4πm/s
Step 4: Relate Velocity Head to Height Difference
The velocity head v22g is converted into elevation head h. Thus, we can write:
h=v22g
Substituting for v:
h=(0.4π)22g
Step 5: Calculate g
Using g≈9.8m/s2:
h=(0.4π)22×9.8
Step 6: Calculate h
Calculating (0.4π)2:
(0.4π)2=0.16π2
Now substituting back into the equation for h:
h=0.16π219.6
Using π2≈9.87:
h≈0.16×9.8719.6≈1.579219.6≈0.0806m≈8.06cm
Final Answer
Thus, the difference in height h between the center and the side of the liquid in the vessel is approximately:
h≈8cm
---
We have a cylindrical vessel with a radius of r=5cm=0.05m that is rotating at n=4rev/s. We need to find the difference in height h between the center and the sides of the liquid in the vessel.
The angular velocity ω in radians per second can be calculated using the formula:
ω=2πn
Substituting the given value:
ω=2π×4=8πrad/s
The linear velocity v at the radius r can be calculated using the formula:
v=ωr
Substituting the values:
v=(8π)×(0.05)=0.4πm/s
The velocity head v22g is converted into elevation head h. Thus, we can write:
h=v22g
Substituting for v:
h=(0.4π)22g
Using g≈9.8m/s2:
h=(0.4π)22×9.8
Calculating (0.4π)2:
(0.4π)2=0.16π2
Now substituting back into the equation for h:
h=0.16π219.6
Using π2≈9.87:
h≈0.16×9.8719.6≈1.579219.6≈0.0806m≈8.06cm
Thus, the difference in height h between the center and the side of the liquid in the vessel is approximately:
h≈8cm
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Multipe Correct
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Assertion-Reasoning
Explore 8 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Subjective
Explore 25 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is 0.05m and the speed of rotation is 2rev/s, find difference in the height of the liquid at the centre of the vessel and its sides.
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
View SolutionA cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure . The radius of vessel is 5 cm and the angular speed of rotation is ω rad s−1. The difference in the height , h ( in cm ) of liquid at the centre of vessel and at the side will be :
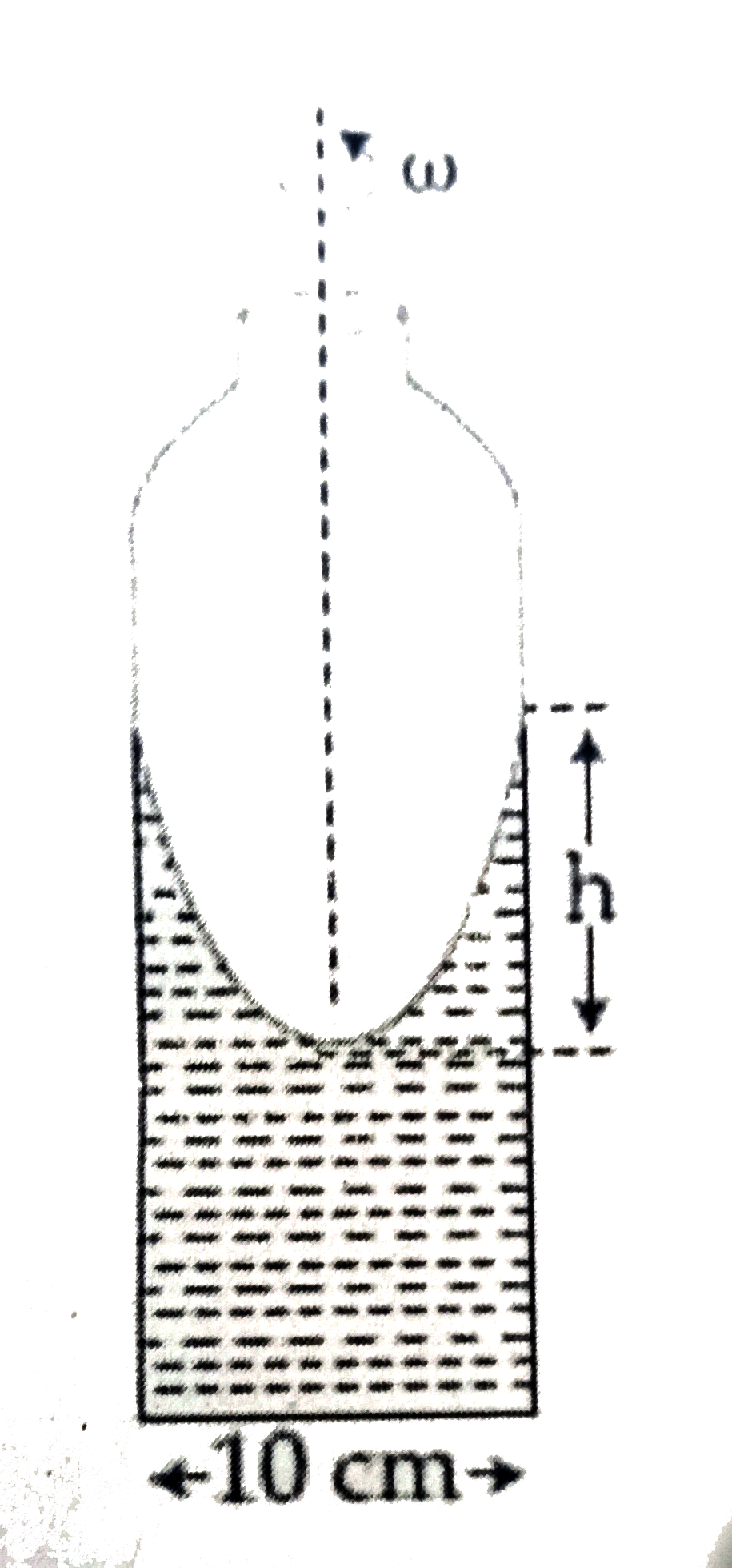
View SolutionA long cylindrical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis, the liquid rises up near the wall. If the radius of vessel is 5 cm and its rotational speed is 2 rotations per second, then the difference in the heights between the centre and the sides, in cm, will be:
View SolutionA cylindrical vessel of radius r containing a liqiud is rotating about a vertical axis through the centre of circular base, If the vessel is rotating with angular velocity ω then what is the difference of the heights of liquid at centre of vessel and edge?
View SolutionA cylinder vessel of radius 10 cm containing a liquid is rotating about a vertical axis through the centre of circular base. The vessel is rotating with angular frequency 10 rad/s. Find the difference of the heights of liquid at centre of vessel and edge.
View SolutionA cylindrical vessel, without lid, has to be tin-coated on its both sides. If the radius of the base is 70cm and its height is 1.4m, calculate the cost of tin-coating at the rate of Rs. 3.50 per 1000 cm2
View SolutionA cylindrical vessel, without lid, has to be tin-coated on its both sides. If the radius of the base is 70cm and its height is 1.4 m, calculate the cost of tin-coating at the rate of Rs. 3.50 per 1000cm2.
View SolutionA cylindrical vessel, without lid, has to be tin-coated on its both sides. If the radius of the base is 70cm and its height is 1.4 m, calculate the cost of tin-coating at the rate of Rs. 3.50 per 1000cm2.
View SolutionA fluid having a thermal coefficient of volume expansion γ is filled in a cylindrical vessel up to a height h0. The coefficient of linear thermal expansion of the material of the vessel is α . If the fluid is heated with the vessel , then find the level of liquid when temperature increases by Δθ.
View Solution