In Young.s double slit experiment intensity at a point is (1/4) of the maximum intensity. Angular position of this points is
I=Imaxcos2(ϕ2)∴Imax4=Imaxcos2(ϕ2)
cos(ϕ)2=12 or ϕ2=π3 ∴ϕ=2π3=(2πλ)△x
where △x=dsinθ
λ3=dsinθ,sinθ=λ3d,θ=sin−1(λ3d).
Topper's Solved these Questions
Similar Questions
Knowledge Check
In Young's double slit experiment intensity at a point is (14) of the maximum intersity. Angular position of this point is
Asin−1(λd)Bsin−1(λ2d)Csin−1(λ3d)Dsin−1(λ4d)In Young's double slit experiment intensity at a point is (14) of the maximum intersity. Angular position of this point is
Asin−1(λd)Bsin−1(λ2d)Csin−1(λ3d)Dsin−1(λ4d)In Young's double - slit experiment intensity at a point is (3/4)th of the maximum intensity. The possible angular position of this point is
Asin−1(λ3d)Bsin−1(λ2a)Csin−1(λ6d)Dsin−1(λ4d)
In Young's double slit experiment,the intensity at a point where the path difference is
View SolutionIn Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is λ and d is the distance between the slits, the angular separation between point P and the center of the screen is
View SolutionYoungs Double slit experiment | variation of intensity on screen
View SolutionIn young's double slit experiment relative intensity at a point on the screen may be defined as ratio of intensity at that point to the maximum intensity on the screen. Light of wavelength 7500∘A A passing through a double slit, produces interference pattern of relative intensity variation as shown in Fig. θ on horizontal axis represents the angular position of a point on the screen
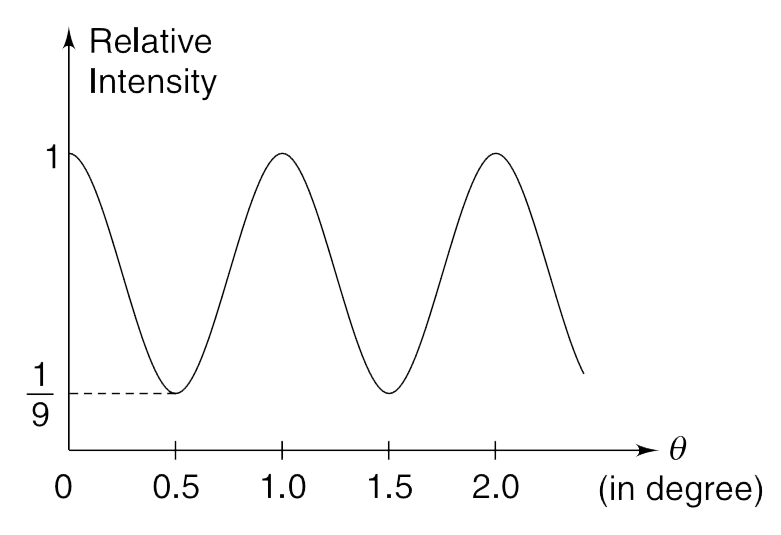
(a) Find separation d between the slits.
(b) Find the ratio of amplitudes of the two waves producing interference pattern on the screen.
View SolutionIn Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is λ and d is the distance between the slits, the angular separation between point P and the center of the screen is
View Solution
