Huygen.s principle of secondary wavelets can be used to
a) deduce the laws of rectraction of light
b) deduce the laws of refraction of light
c) explain the transverse nature of light waves
d) predict the location of a wavefront as time passes
a, b only
a, c only
a, b, d only
b, c only
The correct Answer is:C
Topper's Solved these Questions
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -IA (MATCHING TYPE QUESTIONS)
7 Videos
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -IA (ASCENDING AND DSCENDING ORDER TYPE QUESTIONS)
6 Videos
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -IA (SATEMENT TYPE QUESTIONS)
12 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
Huygen's principle of secondary wavelets may be used to find the velocity of light in vacuum explain the particle behaviour of light find the new position of wavefront explain Snell's law
View SolutionState Huygen's principle for the propagation of light and prove the laws of refraction of light on its basis.
View Solution
Knowledge Check
Huygen was the first scientist who proposed the idea of wave theory of light. He said that the light propagates in form of wavefronts. A wavefront is an imaginary surface at every point of which waves are in the same phase. For example the wavefronts for a point source of light is collectionof concentric spheres which have centre at the origin. w1 is a wavefront. w2 is another wavefront.

The redius of the wavefront at time 't' is 'ct' in this case where 'c' is the speed of light. The direction of propagation of light is perpendicular to the surface of the wavefront. The wavefronts are plane wavefronts in case of a parallel beam of light.

Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be consid-ered only in the forward direction (i.e. the direction of propagation of light) and not in the reverse direction. If a wavefront w1 at time t is given, then to draw the wavefront at time t+Δt0 take some points on the wavefront w1 and draw spheres of radius 'cΔt'. They are called secondary wavelets
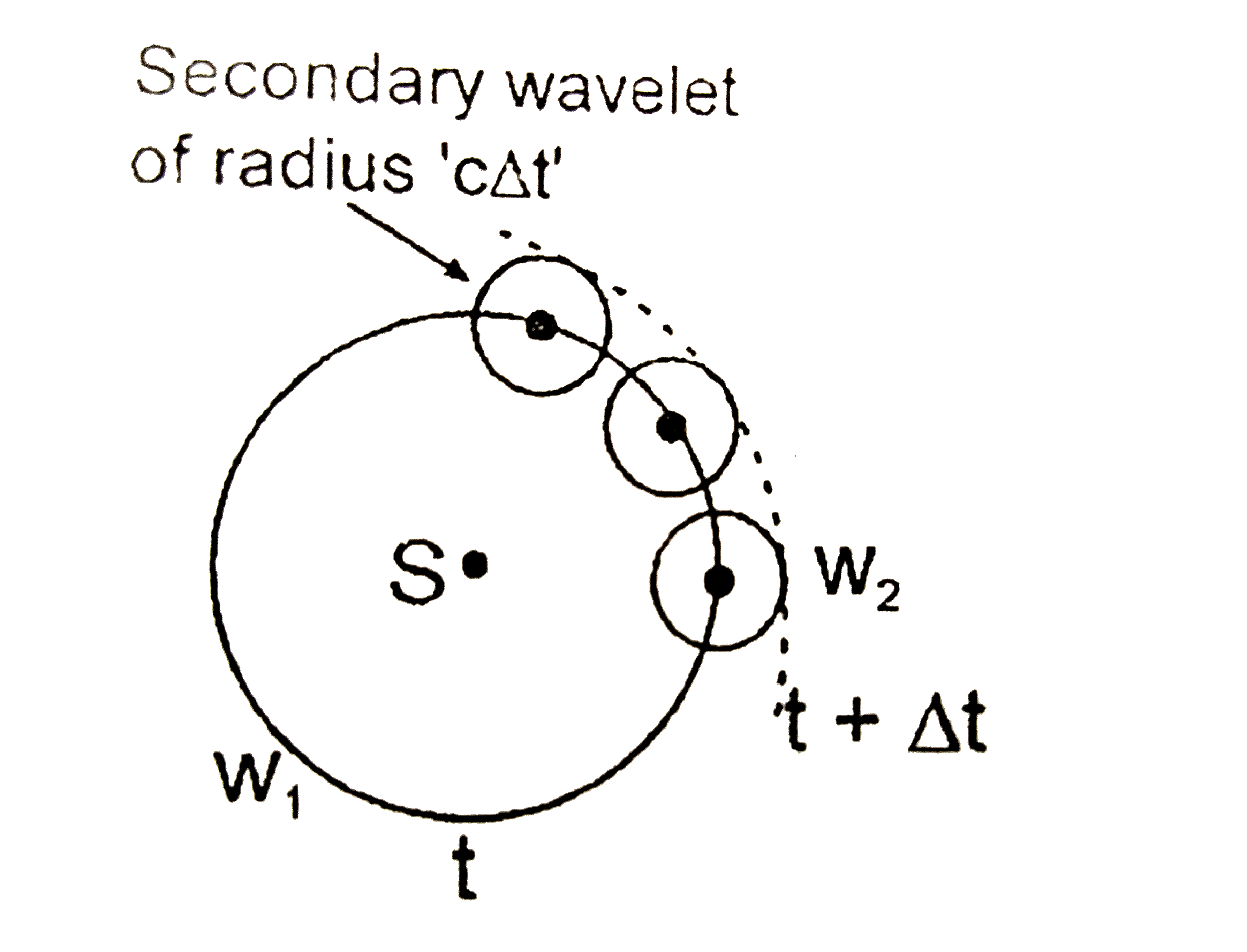
Draw a surface w2 which is tangential to all these secondary wavelets. w2 is the wavefront at time 't+Δt'. Huygen proved the laws of reflection and laws of refraction using concept of wavefronts.
A point source of light is placed at origin, in air. The equation of wave front of the wave at time t, emitted by source at t=0, is (take refractive index of air as 1)Ax+y+z=ctBx2+y2+z2=t2Cxy+yz+zx=c2t2Dx2+y2+z2=c2t2_E01_075_Q01.png)
Huygen was the figure scientist who proposed the idea of wave theory of light he said that the light propagates in form of wavelengths. A wavefront is a imaginary surface of every point of which waves are in the same. phase.
For example the wavefront for a point source of light is collection of concentric spheres which have centre at the origin w1 is a wavefront w2 is another wavefront.
The radius of the wavefront at time 't' is 'ct' in thic case where 'c' is the speed of light the direction of propagation of light is perpendicular to the surface of the wavelength. the wavefronts are plane wavefronts in case of a parallel beam of light.
_E01_075_Q02.png)
Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be considered only in the forward direction (i.e., the direction of propagation of light) and not in the reverse direction if a wavefront w1 and draw spheres of radius 'cΔt' they are called secondary wavelets.
Draw a surface w2 which is tangential to all these secondary wavelets w2 is the wavefront at time t+Δt Huygen proved the laws of reflection and laws of refraction using concept of wavefront.
Q._E01_075_Q03.png)
Spherical wavefronts shown in figure, strike a plane mirror. reflected wavefront will be as shown inA_E01_075_O01.png) B
B_E01_075_O02.png) C
C_E01_075_O03.png) D
D_E01_075_O04.png)
When light passes from a denser medium to a rarer medium
View SolutionUsing Huygens' principle for the wave theory of light, verify the law of refraction.
View SolutionList-I List-II
a) Einstein e) velocity of light
b) Huygen f) diffraction of light
c) Focault g) wave nature of light
d) Fresnel h) particle nature of light
View SolutionHuygen was the first scientist who proposed the idea of wave theory of light. He said that the light propagates in form of wavefronts. A wavefront is an imaginary surface at every point of which waves are in the same phase. For example the wavefronts for a point source of light is collectionof concentric spheres which have centre at the origin. w1 is a wavefront. w2 is another wavefront.

The redius of the wavefront at time 't' is 'ct' in this case where 'c' is the speed of light. The direction of propagation of light is perpendicular to the surface of the wavefront. The wavefronts are plane wavefronts in case of a parallel beam of light.

Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be consid-ered only in the forward direction (i.e. the direction of propagation of light) and not in the reverse direction. If a wavefront w1 at time t is given, then to draw the wavefront at time t+Δt0 take some points on the wavefront w1 and draw spheres of radius 'cΔt'. They are called secondary wavelets
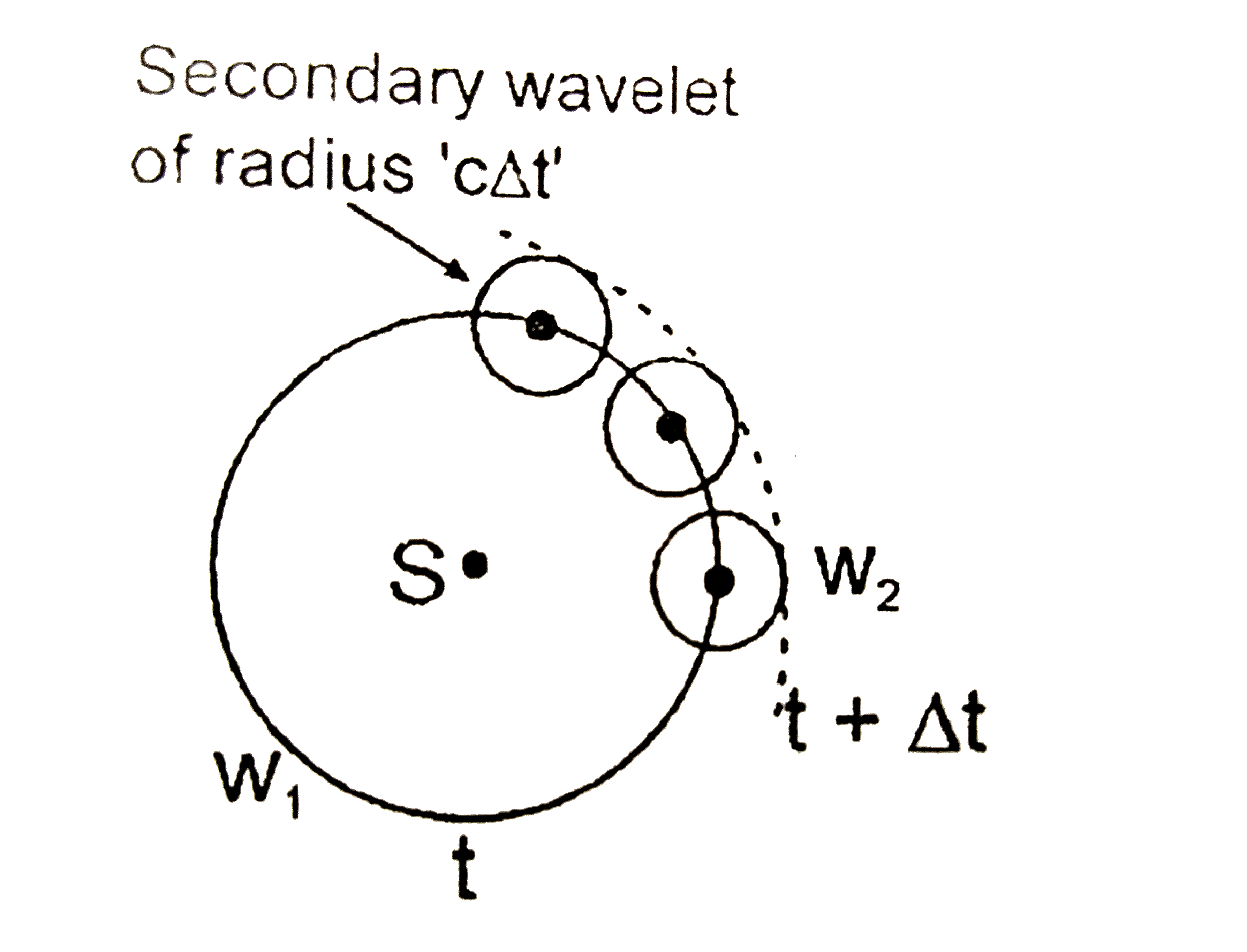
Draw a surface w2 which is tangential to all these secondary wavelets. w2 is the wavefront at time 't+Δt'. Huygen proved the laws of reflection and laws of refraction using concept of wavefronts.
A point source of light is placed at origin, in air. The equation of wave front of the wave at time t, emitted by source at t=0, is (take refractive index of air as 1)
View SolutionUsing Fermat's principle derive the laws of deflection and refraction of light on the plane interface between two media.
View SolutionDeduce Snell's Law of refraction for a plane wave using Huygen's principle.
View Solution
