An electric dipole →P and a point charge q (>0) are located at a separation r as shown. Force on the dipole −−→(F) due to the point charge on the qualitatively dinoted as :





The correct Answer is:D
Topper's Solved these Questions
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -V ELECTRIC DIPOLE) (LEVEL -II LINKED COMPREHENSION TYPE QUESTION)
2 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -V ELECTRIC DIPOLE) (LEVEL -II INTEGER TYPE QUESTION)
1 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -V ELECTRIC DIPOLE) (LEVEL - I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
4 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
6 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
9 Videos
Similar Questions
Knowledge Check
An electric dipole having charges +q and −q at a separation r. At distance d>>r along the axis of the dipole , the field is proportional to
Aqd2Bqrd2Cqd3Dqrd3Two equal charges q of opposite sign separated by a distance 2a constitute an electric dipole of dipole moment p. If P is a point at a distance r from the centre of the dipole and the line joining the centre of the dipole to this point makes an angle θ with the axis of the dipole, then then potential at P is given by (f>>2a) where (p = 2 qa)
AV=pcosθ4πε0r2BV=pcosθ4πε0rCV=psinθ4πε0rDV=pcosθ4πε0r2
A short dipole of dipole moment P is placed near a point charge Q as shown in figure. Find force on the dipole due to the point charge

View SolutionA short dipole of dipole moment P is placed near a point charge Q as shown in figure. Find force on the dipole due to the point charge

View SolutionA spherical shell having charge +Q (uniformly distributed) and a point charge +q0 are placed as shown. Find the force between shell and the point charge (r>>R).
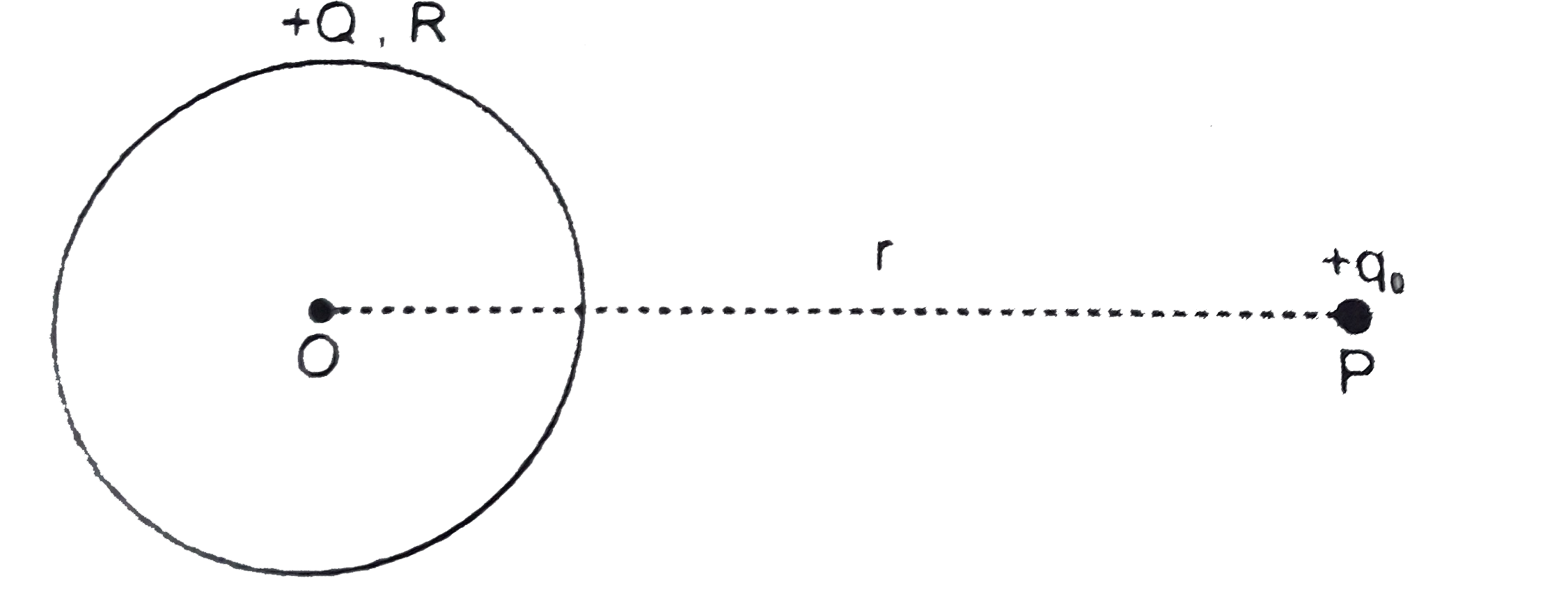
View SolutionAn electric dipole of dipole moment →p consists of point charges + q and - q separated by a distance 2a apart. Deduce the expression for the electric field →E due to the dipole at a distance x from the center of dipole on its axial line in terms of the dipole moment →p . Hence show that in the limit a→0→E=2→p(4πε0x3).
View SolutionA spherical shell having charge +Q (uniformly distributed) and a point charge +q0 are placed as shown. Find the force between shell and the point charge (r>>R).
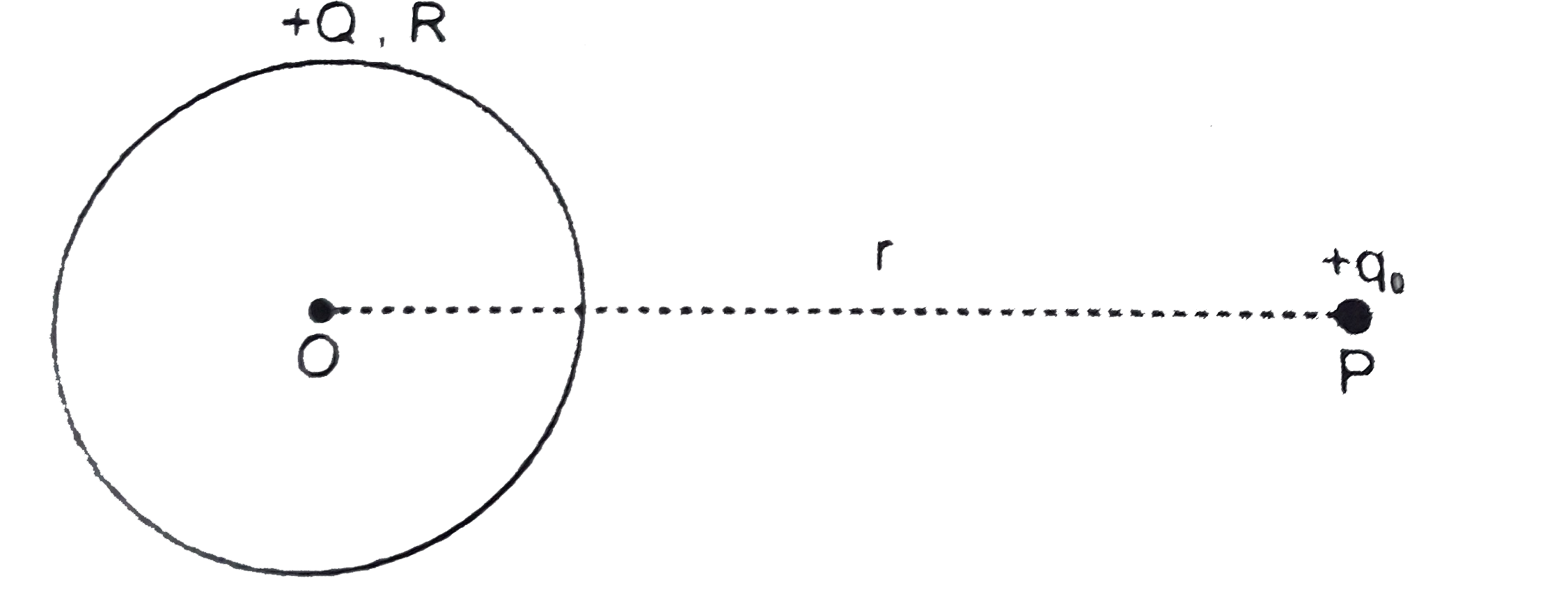
(i) Force on the point charge +q0 due to the shell =q→E0 shell=(q0)(KQr2)ˆr=KQq0r2ˆr where ˆr. is unit vector along OP.
From action - reaction principle, force on the shell due to the point charge will also be : Fshell=KQq0r2(−ˆr)
Conslusion : To find the force on a hollow sphere due to outside charges, we can replace the sphere by a point charge kept at centre.
View SolutionTwo equal charges q of opposite sign separated by a distance 2a constitute an electric dipole of dipole moment p. If P is a point at a distance r from the centre of the dipole and the line joining the centre of the dipole to this point makes an angle θ with the axis of the dipole, then then potential at P is given by (r>>2a) where (p = 2 qa)
View Solution
