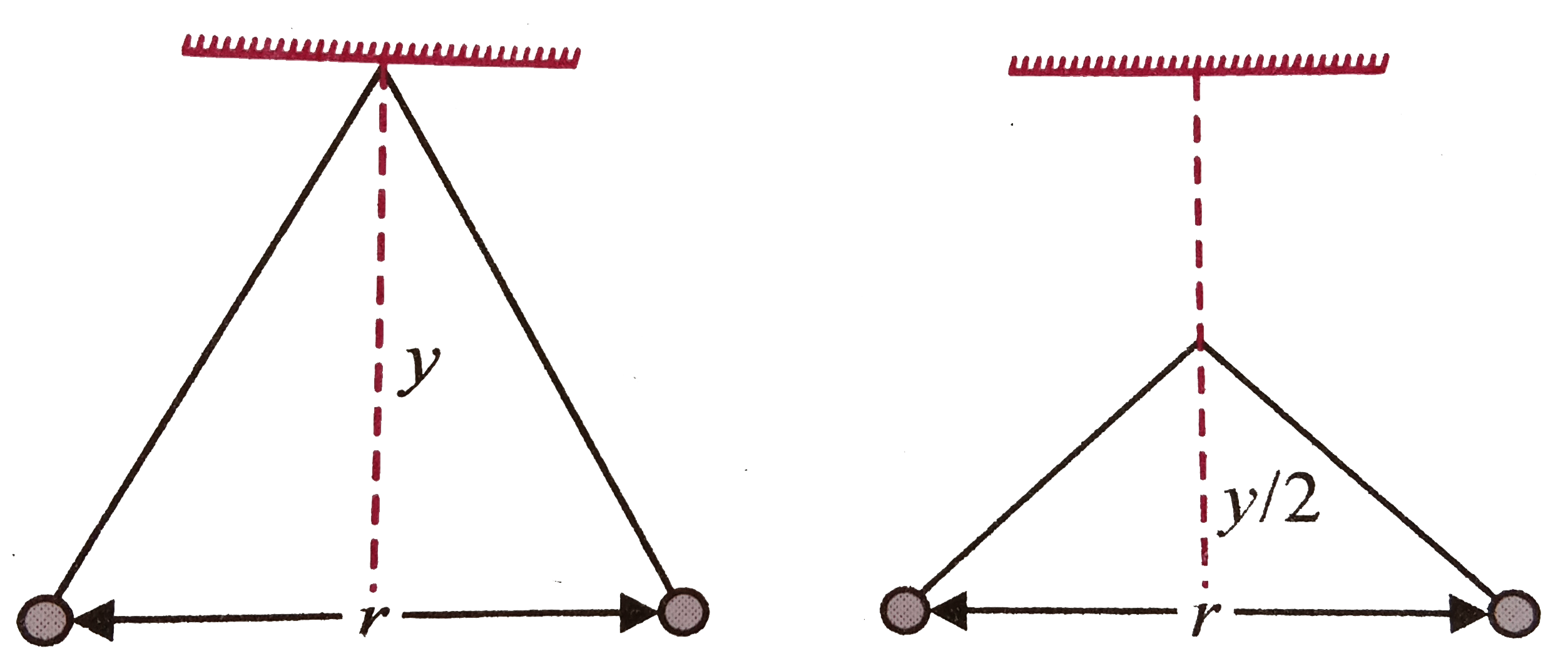
Two identical balls each having a density p are suspended from a common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle $θ$ with the vertical. Now both the balls are immersed in a liquid. As a resultant the angle $θ$ does not change. The density of liquid is $σ$ . Find the dielectric constant of the liquid.

A

$\frac{ρ}{ρ - σ}$

B

$\frac{σ}{ρ - ρ}$

C

$\frac{ρ - σ}{ρ}$

D

$\frac{ρ - σ}{σ}$

Text Solution

Verified by Experts

The correct Answer is:A

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two small identical balls are suspened from a common point by two identical strings. When they are given identical charges, they move apar and the strings make with the vertical an angle of q. Now the system is immersed in a liquid and as a result the angle q does not change. If r is the density of the material of the balls and s is the density of the liquid, the dielectric constant of the liquid is
A $\frac{p}{p - σ}$
B $\frac{p - σ}{p}$
C $\frac{σ}{p - σ}$
D $\frac{p - σ}{σ}$
Question 2 - Select One
Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle $' θ'$ with the vertical ?
A $x = {(\frac{q^{2} l}{2 π ε_{0} m g})}^{1 / 2}$
B $x = {(\frac{q^{2} l}{2 π ε_{0} m g})}^{1 / 3}$
C $x = {(\frac{q^{2} l^{2}}{2 π ε_{0} m^{2} g})}^{1 / 3}$
D $x = {(\frac{q^{2} l^{2}}{2 π ε_{0} m^{2} g^{2}})}^{1 / 3}$

AAKASH SERIES-ELECTROSTATICS-ADDITIONAL PRACTICE EXERCISE (LEVEL - I (MAIN) (STRAIGHT OBJECTIVE TYPE QUESTIONS)

Home
Ask Doubt
Profile