A particle of charge -q and mass m moves in a circle aroung a long wire of linear charge density . If r = radius of the circular path and T = time period of the motion circular path. Then :
The correct Answer is:A
Topper's Solved these Questions
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
20 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
5 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -V ELECTRIC DIPOLE) (LEVEL -II INTEGER TYPE QUESTION)
1 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
6 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
9 Videos
Similar Questions
A particle of charge −q and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density +λ. Then, time period will be
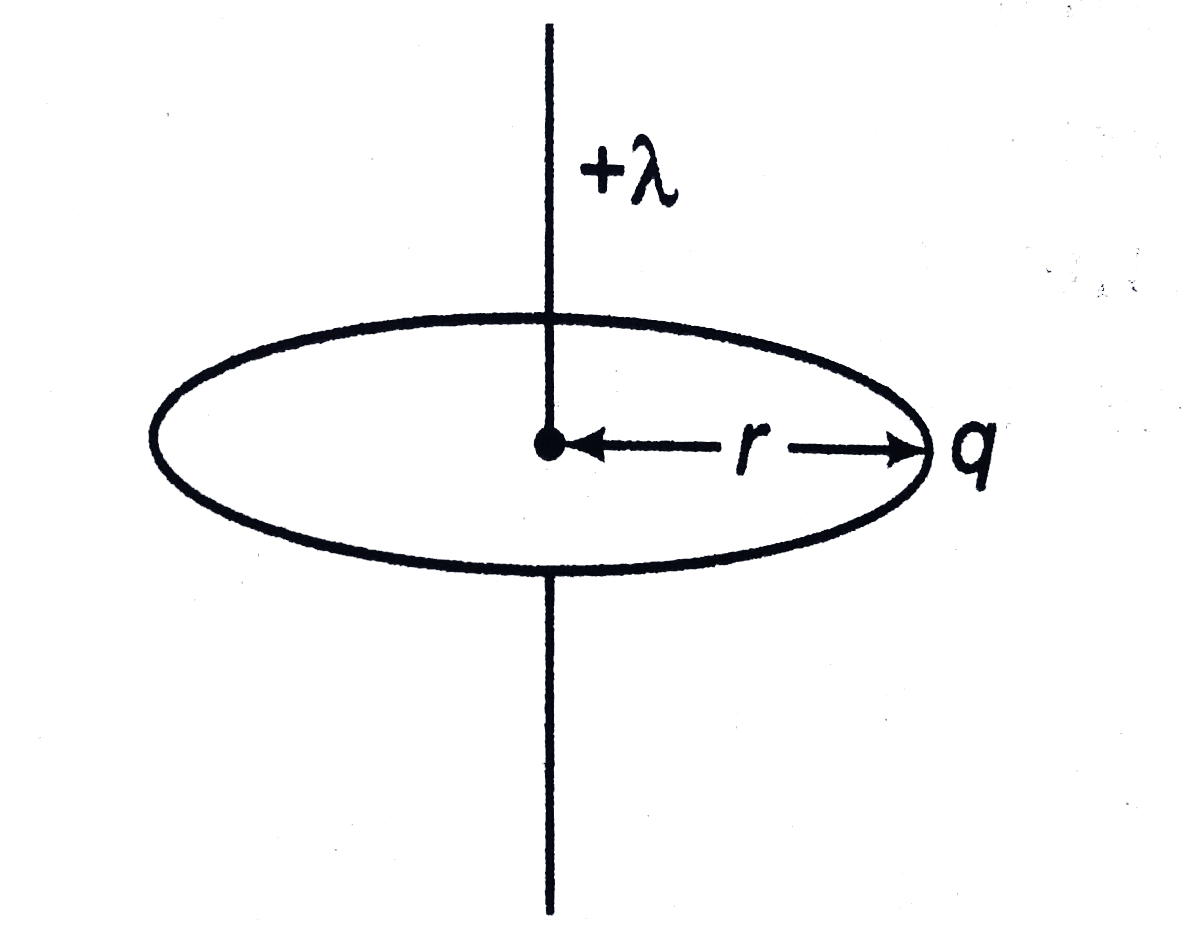 where , k=14πε0)
where , k=14πε0)
View SolutionA particle of charge q1 and mass m is revolving around a fixed negative charge of magnitude q2 in a circular path of radius r. Find the time period of revolution.
View Solution
Knowledge Check
A particle of charge −q and mass m moves in a circular orbits of radius r about a fixed charge +Q.The relation between the radius of the orbit r and the time period T is
Ar=Qq16π2ε0MT3Br3=Qq16π2ε0MT2Cr2=Qq16π3ε0mT3Dr2=Qq16π3ε0mT3A particle of charge −q and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density +λ. Then, time period will be
 where , k=14πε0)AT=2πr√(m2kλqBT2=4π2m2kλqr3CT=12πr√2kλwmDT=12πr√m2kλq
where , k=14πε0)AT=2πr√(m2kλqBT2=4π2m2kλqr3CT=12πr√2kλwmDT=12πr√m2kλqIf a charge particle of charge q , mass m , moves in a circular path in magnetic field of induction B , under a potential of V volts then radius of circular path is
A√2mVqBB1√2mVqC1B√2mVqD1B2√2mVq
A charge particle is moving in a uniform magnetic field ib a circular path. The energy of the particle is doubled . If the initial radius of he circular path was R, the radius of the new circular path after the energy is doubled will be
View SolutionA particle of charge -q and mass m moves in a circular orbit about a fixed charge +Q. Show that the r3αT2 law, is satisfied, where r is the radius of orbit and T is time period.
View SolutionA charge 'q' of opposite nature is revolving round an infinitely long linear charge of density λ C/m in a circular orbit of radius 'r'.The speed of the revolving charge will be
View SolutionA charge particle is moving in a uniform magnetic field ib a circular path. The energy of the particle is doubled . If the initial radius of he circular path was R, the radius of the new circular path after the energy is doubled will be
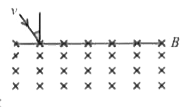
View SolutionA charged particle of charge q and mass m enters a magnetic field as shown. Find radius of the circular path and the time spent inside the field. Neglect gravity.
View Solution
