The cross-section area and length of cylindrical conductor are A and l respectively. The specific conductivity varies as σ(x)=σ0l√x, where x is the distance along the axis of the cylinder from one of its ends. Compute the resistance of the system along the cylindrical axis.
3√l2Aσ0
2l3Aσ0
2√l3Aσ0
√lAσ0
The correct Answer is:C
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - LECTURE SHEET (EXERCISE- II LEVEL- II (ADVANCED) (Linked Comprehension Type Questions))
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - LECTURE SHEET (EXERCISE- II LEVEL- II (ADVANCED) (Matrix Matching Type Questions))
1 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - LECTURE SHEET (EXERCISE- II LEVEL-I (MAIN) (Straight Objective Type Questions))
14 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
44 Videos
Similar Questions
A cylindrical conductor of length l and radius a has conductivity near its axis as σ. The conductivity of material increases linearly with the distance from axis and becomes 2σ near the surface.The resistance of conductor for longitudinal current is
View SolutionThe resistivity of cylindrical conductor carrying steady current along its length varies linearly with the distance from the current carrying end as given by ρ=ρ0(1+xl) where l is the length of the conductor and x is the distance from the current entry and. ρo is a positive constant.
View Solution
Knowledge Check
A cylindrical conductor AB of length l and area of cross-section a is connected to a battery having emf E and negligible internal resistance. The specific conductivity of cylindrical conductor varies as σ=σ01√x, where σ0 is constant and x is distance from end A. What is the electric field just near the end B of cylinder?
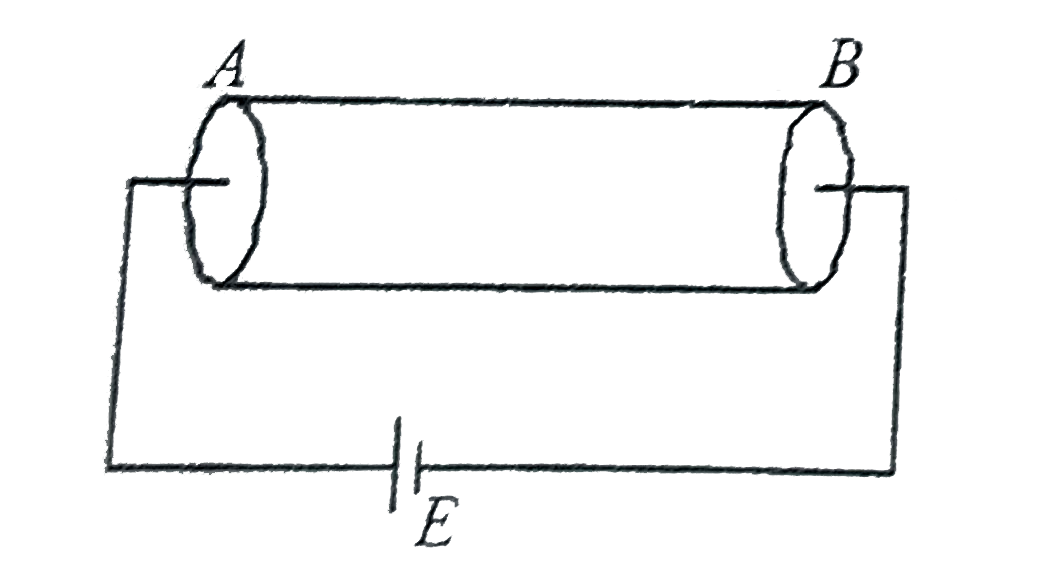 AElB3E2lC2E3lDE2l
AElB3E2lC2E3lDE2lA solid cylinder of length l and cross-sectional area A is made of a material whose resistivity depends on the distance r from the axis of the cylinder as ρ=k/r2 where k is constant . The resistance of the cylinder is -
AπklA2B2πklA2CπklADNoneA solid cylindrical wire of length l has cross-section radius a as shown below. The specific resistance of material is given as ρ=ρ0r, where r is distance from axis of cylinder and ρ0 is a positive constant quantity. The resistance across its ends is :
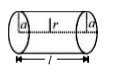 Aρ0l2πaBρ0lπa2Cρ0lπaD2ρ0lπ
Aρ0l2πaBρ0lπa2Cρ0lπaD2ρ0lπ
The specific resistance of a material of wire changes as ρ=ρ0x along the length of the conductor whose area of cross section is constant and equal to A. Here x is the distance of point on conductor from one end of the wire. Calculate its electric resistance. (Given the length of the wire is L)
View SolutionA long cylindrical conductor of radius R having a cylindrical cavity of radius R/2 through out its length is lying with its axis parallel to x-axis. The distance between the axes of the cylinder and the cavity length in the positive x direction. The across sectional view of the cylinder is shown in the figure

The magnetic induction at point on the cavity is
View SolutionA cylindrical conductor has length l and area of cross section A. Its conductivity changes with distance (x) from one of its ends as σ=σ0lx.[σ0is a constant]. Calculate electric field inside the conductor as a function of x, when a cell of emf V is connected across the ends.
View SolutionA conductor of length l and area of cross-section A has a resistance R then its specific resistance is
View SolutionA long cylindrical conductor of radius R having a cylindrical cavity of radius R/2 through out its length is lying with its axis parallel to x-axis. The distance between the axes of the cylinder and the cavity length in the positive x direction. The across sectional view of the cylinder is shown in the figure

The magnetic induction at point on the cavity is
View Solution
