In the above problem, compute the current density if the potential drop along the cylinder is V0. Also find the electric field at each point in the cylinder in the case described?
32σ0V0l,32V0xl3/2
σ0V0√x,V0√x2l3/2
23σ0V0√x,23V0√xl3/2
3σ0V02√l,3V0√x2l3/2
The correct Answer is:D
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - LECTURE SHEET (EXERCISE- II LEVEL- II (ADVANCED) (Linked Comprehension Type Questions))
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - LECTURE SHEET (EXERCISE- II LEVEL- II (ADVANCED) (Matrix Matching Type Questions))
1 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - LECTURE SHEET (EXERCISE- II LEVEL-I (MAIN) (Straight Objective Type Questions))
14 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
44 Videos
Similar Questions
A current I flows along a thin-walled, long, half-cylinder of radius R(figure) Find the magnetic induction at a point on the axis of the cylinder
View Solution(a) There is a long uniformly charged cylinder having a volume charge density of ρC/m3. Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.
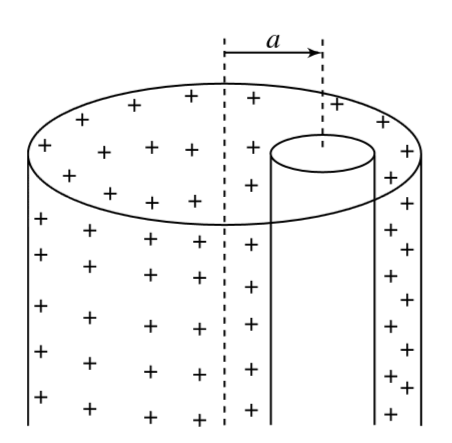
View Solution
Knowledge Check
The electric potential at any point x,yanz in metres is given by V=3x2. The electric field at a point (2,0,1) is
A12 Vm−1B−6 Vm−1C6 Vm−1D−12 Vm−1If the linear charge density of a cylinder is 4μCm−6 ,then electric field intensity at point 3.6 cm from axis is :
A4×105NC−1B2×106NC−1C8×107NC−1D12×107NC−1A very long uniformly charged cylinder (radius R) has a surface charge density σ . A very long uniformly charged line charge( linear charge density λ) is placed along the cylinder axis. If electric field intensity vector outside the cylinder is zero then :
Aλ=RσBλ=−RσCλ=2πRσDλ=−2πRσ
Consider the situation described in the previous problem. Suppose the current I enters the loop at the point A and leaves it at the point B. Find the magnetic field at the centre of the loop.
View SolutionIf the linear charge density of a cylinder is 4μCm−6 ,then electric field intensity at point 3.6 cm from axis is :
View SolutionA very long uniformly charged cylinder (radius R) has a surface charge density σ . A very long uniformaly charged line charge( linear charge density λ) is placed along the ctlinder axis. If electric field intensity vector outside the cylinder is zerom then :
View SolutionLet V0 be the potential at the origin in an electric field →E=4ˆi+5ˆj. The potential at the point (x,y) is
View SolutionLet V0 be the potential at the origin in an electric field →E=4ˆi+5ˆj. The potential at the point (x,y) is
View Solution
