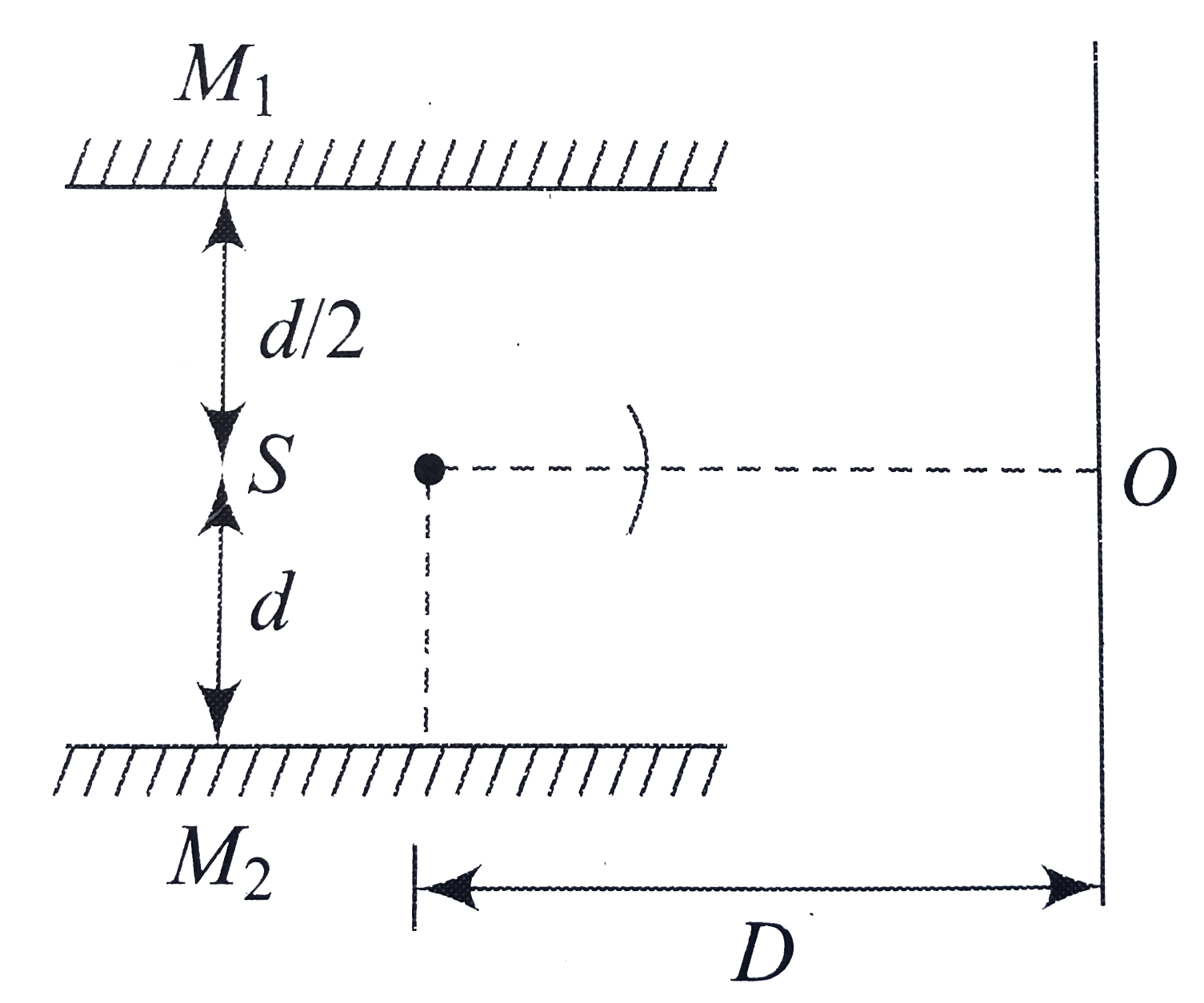
M1andM2 are plane mirrors and kept parallel to each other . At point O , there will be a maxima for wavelength . Light from a monochromatic source S of wavelength λ is not reaching directly on the screen . Then λ is

3d2D
3d22D
d2D
2d2D
The correct Answer is:B
Topper's Solved these Questions
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED ) More than one correct answer Type Questions
4 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED ) Linked Comprehension Type Questions
7 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET EXERCISE-I (LEVEL -I) (MAIN) straight objective Type Questions
16 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
81 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
_E01_047_Q01.png)
M1 and M2 are plane mirrors and kept parallel to each other. At point O there will be a maxima for wavelength λ. Light from monochromatic source S of wavelength λ is not reaching directly on the screen then λ is [D>>d>>λ]
View SolutionM1 and M2 are plane mirrors and kept parallel to each other. At point O, there will be a maxima for wavelength λ. Light from a monochromatic sources S of wavelength λ is not reaching directly on the screen. Then, λ is
View Solution
Knowledge Check
M1 and M2 are plane mirrors and kept parallel to each other. At point O, there will be a maxima for wavelength λ. Light from a monochromatic sources S of wavelength λ is not reaching directly on the screen. Then, λ is
 A3d2DB3d22DCd2DD2d2D
A3d2DB3d22DCd2DD2d2DM1 and M2 are two plane mirrors which are kept parallel to each other as shown. There is a point 'O' on perpendicular screen just infront of 'S'. What should be the wavelength of light coming from monchromatic source 'S'. So that a maxima is formed at 'O' due to interference of reflected light from both the mirrors. [Consider only 1st reflection]. [D>>d,d>>λ]
 A3d2DB3d22DCd2DD2d2D
A3d2DB3d22DCd2DD2d2DA beam o monochromatic light of wavelength λ is reflected from air into water to refractive index 4/3. The wavelength of light beam inside water will be
A916×λB3λ/4Cλ×43Dλ
M1 and M2 are two plane mirrors which are kept parallel to each other as shown. There is a point 'O' on perpendicular screen just infront of 'S'. What should be the wavelength of light coming from monchromatic source 'S'. So that a maxima is formed at 'O' due to interference of reflected light from both the mirrors. [Consider only 1st reflection]. [D>>d,d>>λ]

View SolutionA beam o monochromatic light of wavelength λ is reflected from air into water to refractive index 4/3. The wavelength of light beam inside water will be
View SolutionTwo mirror M1 and M2 make an angle ϕ with line AB. A point source S is kept at a distance r from the point of intersection of mirror. A small hemispherical annular mask is kept close to S so that no ray emanting from S directly reaches the screen kept at a distance b from the source. Interference pattern of rays reflected from M1 and M2 is oberved on the screen. Find the fringe width of this interference pattern λ= wavelength of light being emitted by source.
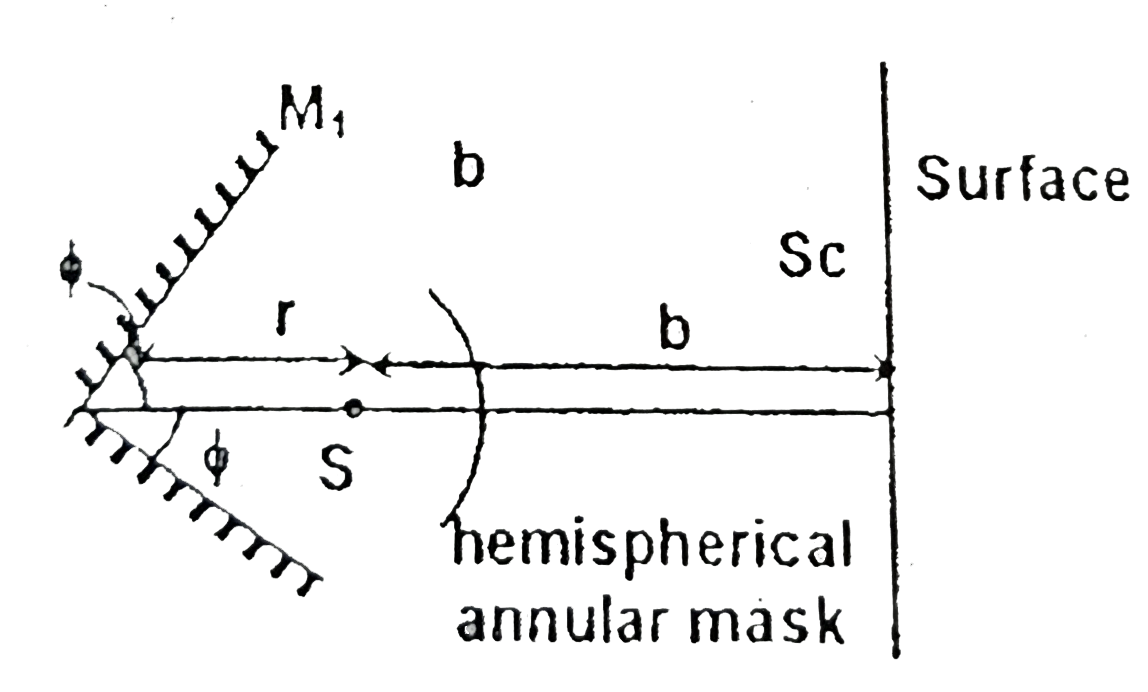
View SolutionTwo mirror M1 and M2 make an angle ϕ with line AB. A point source S is kept at a distance r from the point of intersection of mirror. A small hemispherical annular mask is kept close to S so that no ray emanting from S directly reaches the screen kept at a distance b from the source. Interference pattern of rays reflected from M1 and M2 is oberved on the screen. Find the fringe width of this interference pattern λ= wavelength of light being emitted by source.

View SolutionThree coherent point sources S1,S2andS3 are placed on a line perpendicular to the screen as shown in the figure. The wavelength of the light emitted by the sources is lambda. The distance between adjacent sources is d=3λ The distance of S2 from the screen is D(>>λ). Find the minimum (non zero) distance x of a point P on the screen at which complete darkness is obtained.

View Solution
