![M(1) and M(2) are plane mirrors and kept parallel to each other. At point O there will be a maxima for wavelength lamda. Light from monochromatic source S of wavelength lamda is not reaching directly on the screen then lamda is [Dgt gt d gt gt lamda]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_C08(III)_E01_047_Q01.png)
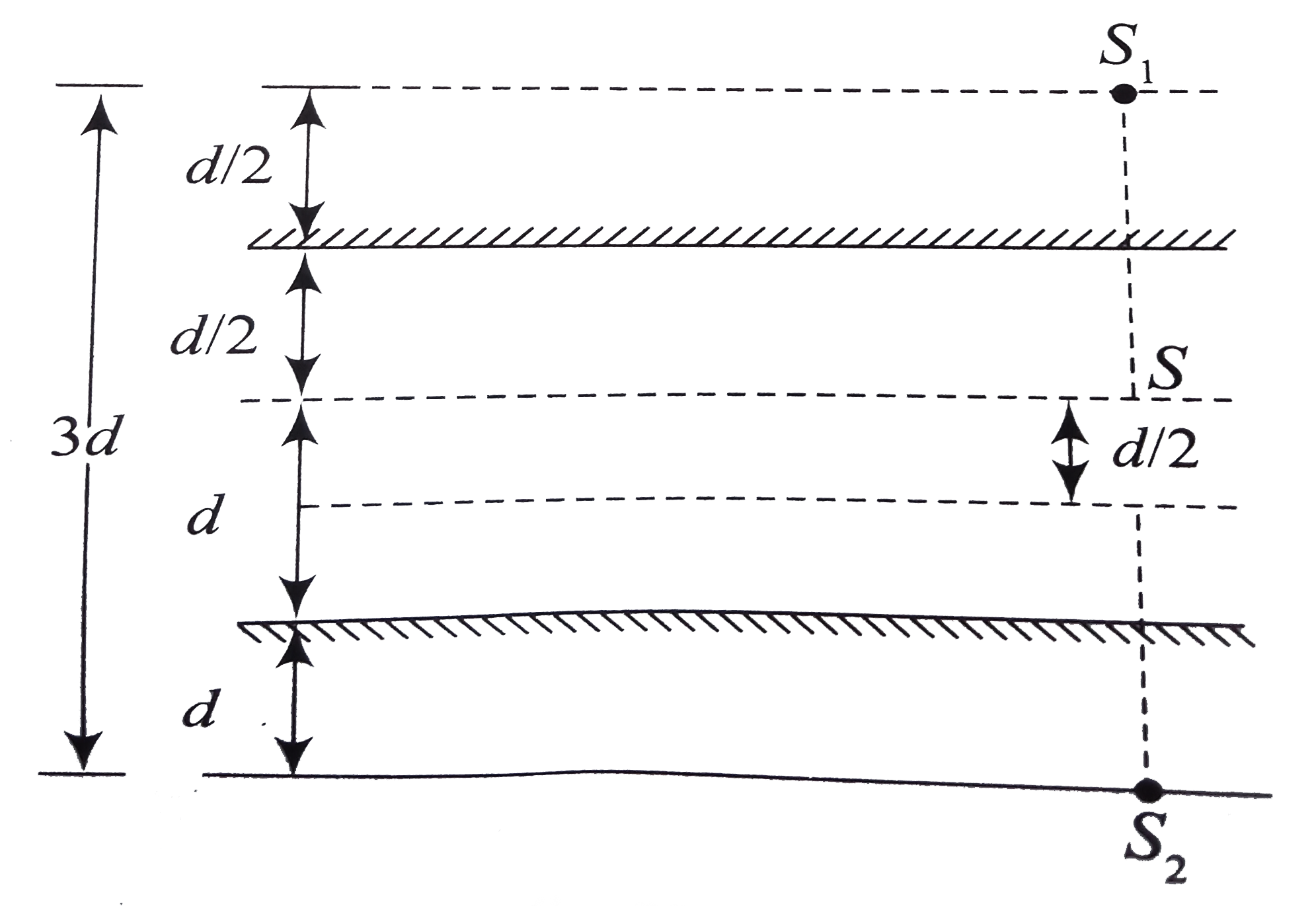
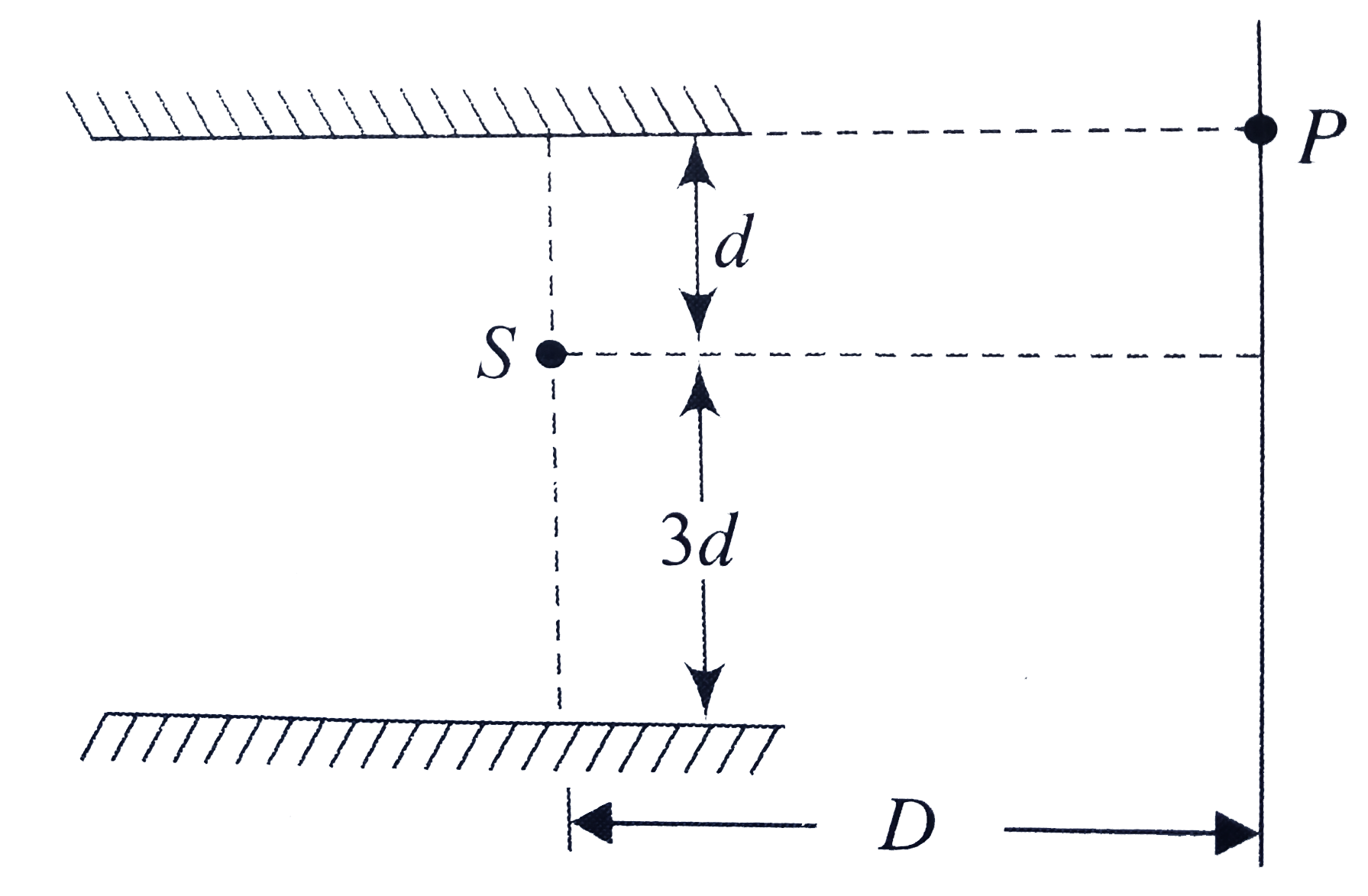
M1 and M2 are plane mirrors and kept parallel to each other. At point O there will be a maxima for wavelength λ. Light from monochromatic source S of wavelength λ is not reaching directly on the screen then λ is [D>>d>>λ]
3d2D
3d22D
d2D
2d2D
The correct Answer is:b
The situation can be taken as if there are two sources S1 and S2 as shown in the figure in question.
For 'O' to be a maxima:
Path difference (3d)(d/2)D=3dd2D=nλ
⇒λ=3d22nD or λ=3d22D
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct8videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning13videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Subjective11videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
Similar Questions
_E01_047_Q01.png)
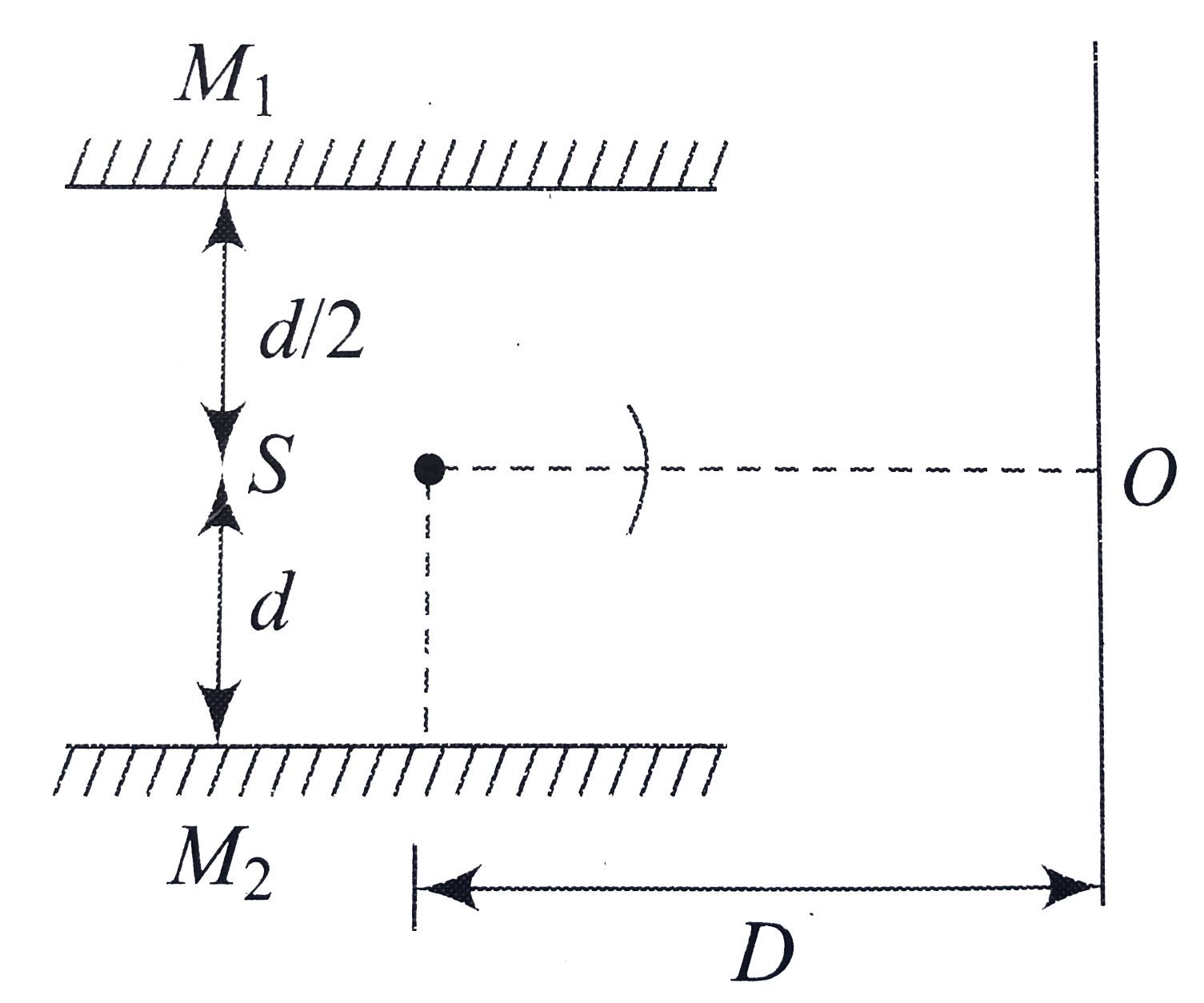
M1 and M2 are plane mirrors and kept parallel to each other. At point O there will be a maxima for wavelength λ. Light from monochromatic source S of wavelength λ is not reaching directly on the screen then λ is [D>>d>>λ]View SolutionM1 and M2 are plane mirrors and kept parallel to each other. At point O, there will be a maxima for wavelength λ. Light from a monochromatic sources S of wavelength λ is not reaching directly on the screen. Then, λ is
 View Solution
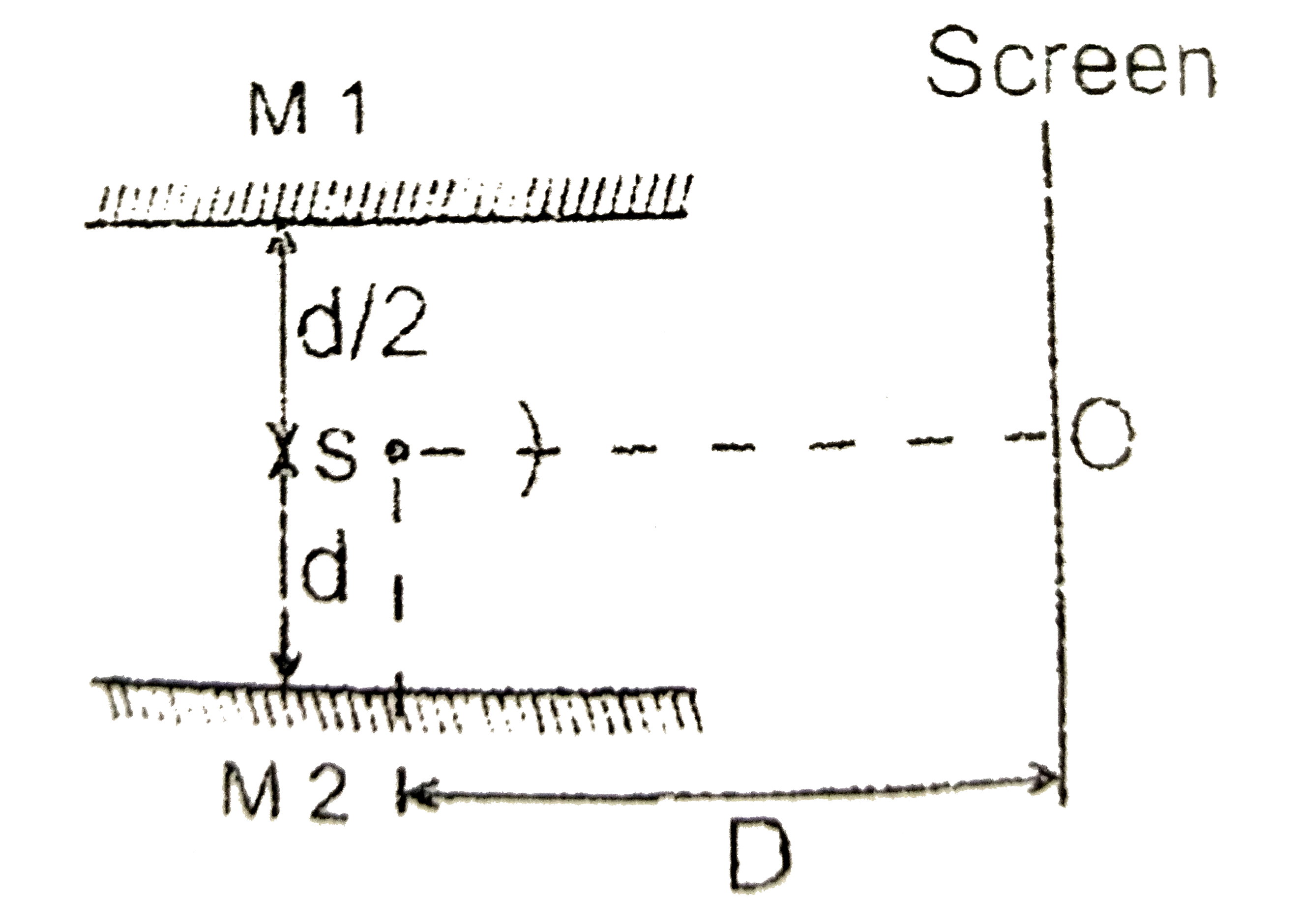
View SolutionM1 and M2 are two plane mirrors which are kept parallel to each other as shown. There is a point 'O' on perpendicular screen just infront of 'S'. What should be the wavelength of light coming from monchromatic source 'S'. So that a maxima is formed at 'O' due to interference of reflected light from both the mirrors. [Consider only 1st reflection]. [D>>d,d>>λ]
 View Solution
View SolutionIn the Young's double slit experiment using a monochromatic light of wavelength λ, the path difference (in terms of an integer n) corresponding to any point having half the peak
View SolutionIn the Young's double slit experiment using a monochromatic light of wavelength λ, the path difference (in terms of an integer n) corresponding to any point having half the peak
View SolutionIn a Young's double slit experiment, the slit separation is 1mm and the screen is 1m from the slit. For a monochromatic light of wavelength 500nm, the distance of 3rd minima from the central maxima is
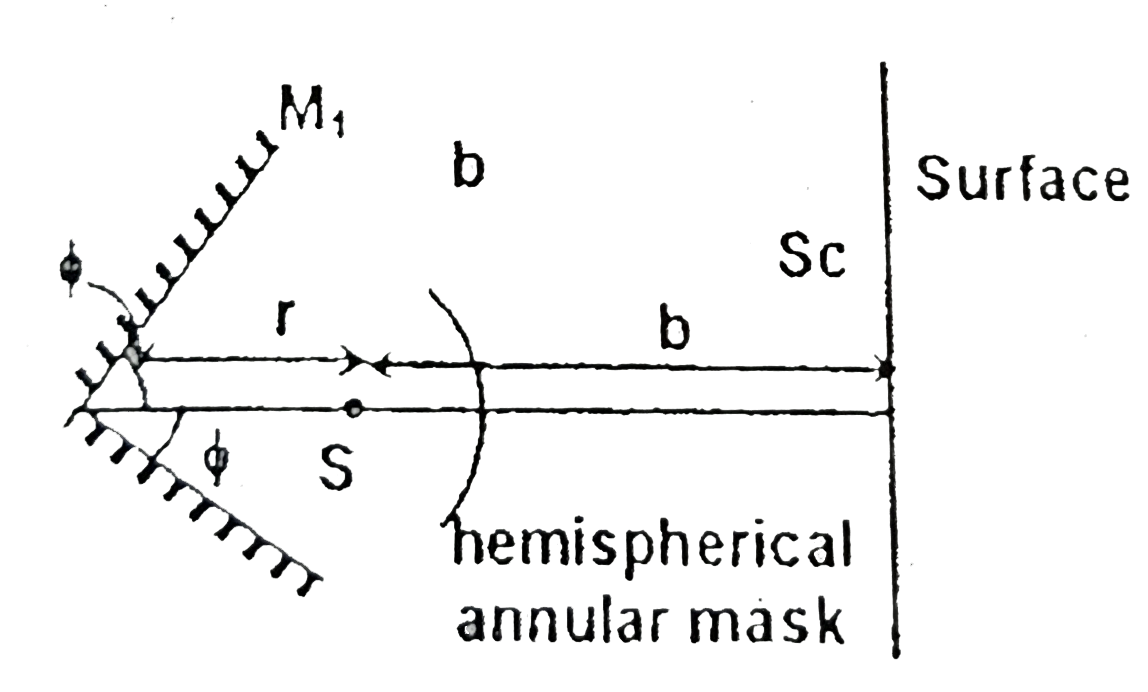
View SolutionTwo mirror M1 and M2 make an angle ϕ with line AB. A point source S is kept at a distance r from the point of intersection of mirror. A small hemispherical annular mask is kept close to S so that no ray emanting from S directly reaches the screen kept at a distance b from the source. Interference pattern of rays reflected from M1 and M2 is oberved on the screen. Find the fringe width of this interference pattern λ= wavelength of light being emitted by source.
 View Solution
View SolutionThe angles of incidence and refraction of a monochromatic ray of light of wavelength λ at an air-glass interface are i and r, respectively. A parallel beam of light with a small spread δλ in wavelength about a mean wavelength λ is refracted at the same air-glass interface. The refractive index μ of glass depends on the wavelength λ as μ(λ)=a+b/λ2 where a and b are constants. Then the angular spread in the angle of refraction of the beam is
View SolutionConsider the optical system shown in figure. The point source of ligth S is having wavelength equal to λ. The light is reaching screen only after reflection. For point P to be socond maxima, the value of λ would be (D>>d and d>>λ)
 View Solution
View SolutionConsider the optical system shown in figure. The point source of ligth S is having wavelength equal to λ. The light is reaching screen only after reflection. For point P to be socond maxima, the value of λ would be (D>>d and d>>λ)
 View Solution
View Solution

