A slit 5.0 cm wide is irradiated normally with microwaves of wavelength 1.0 cm. Then the angular spread of the central maximum on either side of the incident light is nearlySolution in Telugu
15 radian
5 radian
4 radian
6 radian
The correct Answer is:A
Step by step video, text & image solution for A slit 5.0 cm wide is irradiated normally with microwaves of wavelength 1.0 cm. Then the angular spread of the central maximum on either side of the incident light is nearly by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET EXERCISE-II (LEVEL -II) (MAIN) (Straight Objective Type Questions)8videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET EXERCISE-III (LEVEL -I) (MAIN) (Straight Objective Type Questions)9videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET EXERCISE-I (LEVEL -II) (ADVANCED ) Interger Type Questions1videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)81videos
WAVE MOTION AND SOUND
- BOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)15videos
WAVES
Similar Questions
In a Fraunhoffer diffraction experiment at a single slit using light of wavelength 400 nm, the first minimum is formed at an angle of 30∘. Then the direction θ of the first secondary maximum is
01:08View SolutionFrom brewster's law for polarisation, it follows that the angle polarisation depends upon
02:15View SolutionIn the YDSE the monochronic source of wavelength λ is palced at a distance d2 from the central axis (as shown in the figure ) , where d is the separation between two slits S1andS2 .Find the position of the central maxima . (Given d = 6 mm )
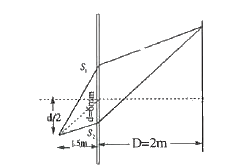 View Solution
View SolutionA wave is described by the equation
y=(1.0mm)sinπ(x2.0cm−10.01s)
Find the time period and the wavelength.View SolutionWhen a train is approaching the stationary observer, the apparent frequency of the whistle observed as 100 Hz, while when it has passed away from the observer with same speed, it is 50 Hz. Calculate the frequency of the whistle when the observer moves with the train (V = 330 m/s)
02:01View SolutionA slit 5 cm wide when irradiated by waves of wavelength 10 mm results in the angular spread of the central maxima on either side of incident light by about :
01:56View SolutionA slit 4.0 cm wide is irradiated with microwaves of 2.0 cm. Find the angular spread of central maximum assuming incidence normal to the plane of the slit.
01:27View SolutionMicrowaves of frequency 24,000 MHz are incident normally on a rectengular on a rectangular slit of width 5 cm. Calculate the angular spread of the central maximum of the diffraction pattern of the slit.
05:17View SolutionA slit 4.0 cm wide is irradiated with microwaves od wavelengths 2.0 cm. Find the angular spread of the central maximum, assuming incidence normal to the plane of the slit.
02:26View SolutionA slit whose width is 5.0 cm is irradiated with microwaves of wavelength 3 cm. What is the angular spread of the central maximum? Assume normal incidence.
04:28View SolutionA microwave of wavelength 2 cm falls normally on a narrow slit of width 5 cm. what is the angular width of central maximum on either side of it?
02:26View SolutionA slit 4 cm wide is irradiated with microwaves of wavelength 2 cm. Find the angular spread of central maxima assuming incidence normal to the plane of the slit.
View SolutionA slit 5.0 cm wide is irradiated normally with microwaves of wavelength 1.0 cm. Then the angular spread of the central maximum on either side of the incident light is nearly
01:36View SolutionA slit whose width is 5.0 cm is irradiated with microwaves of wavelength 2 cm. The angular spread of the central maximum ? (Assume that the incidence is along the normal to the plane of the slit) is
02:15View SolutionA slit 5 cm wide is irradiated normally with microwaves of wavelength 1.0 cm. Then the angular instead of central maximum on either side of incident light is nearly
View Solution

