The displacement of two interfering light waves are y1=4sinωt and y2=3cosωt. The amplitude of the resultant wave is (y1 and y2 are in CGS system)Solution in Telugu
5 cm
7 cm
1 cm
zero
The correct Answer is:A
Step by step video, text & image solution for The displacement of two interfering light waves are y_(1) = 4 sin omega t and y_(2) = 3 cos omega t. The amplitude of the resultant wave is (y_(1) and y_(2) are in CGS system) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PRACTICE SHEET EXERCISE -I (LEVEL II - ADVANCED)(Straight Objective Type Questions)
9 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PRACTICE SHEET EXERCISE -I (LEVEL II - ADVANCED)(More than one correct answer Type Questions)
2 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET EXERCISE-III (LEVEL -II) (MAIN) (Straight Objective Type Questions)
8 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
81 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
A beam of light consisting of two wavelength , 6500A∘ and 5200A∘ is used to obtain interference fringes in a Young's double slit experiment (1Å=10−10m). The distance between the slits 2.0 mm and the distance between the plane of the slits and the screen is 120 cm. Find the distance of the third bright fringe on the screen from the central maximum for the wavelength 6500Å.
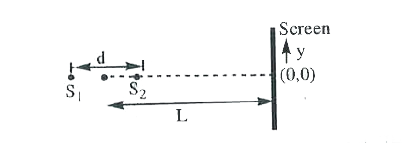
View SolutionThe figure shows two points source which emit light of wavelength λ in phase with each other and are at a distance d=5.5λ apart along a line which is perpendicular to a large screen at a distance L from the centre of the source. Assume that d is much less than L. Which of the following statement is (are) correct ?
View SolutionUnpolarised light of intensity 32 Wm−2 passes through three polarisers such that the transmission axis of the last polariser s crossed with first . If the intensity of the emerging light is 32Wm−2 , the angle between the axes of the first two polarisers is
View SolutionA wave is described by the equation
y=(1.0mm)sinπ(x2.0cm−10.01s)
Find the time period and the wavelength.
View SolutionWhen a train is approaching the stationary observer, the apparent frequency of the whistle observed as 100 Hz, while when it has passed away from the observer with same speed, it is 50 Hz. Calculate the frequency of the whistle when the observer moves with the train (V = 330 m/s)
View SolutionTwo light waves are represented by y_(1)=a sin_(omega)t and y_(2)= a sin(omega t+delta) . The phase of the resultant wave is
View SolutionThe displacements of two intering lightwaves are y_(1) = 4 sin omega t and y_(2) = 3 cos(omega t) . The amplitude of the resultant wave is ( y_(1) and y_(2) are in CGS system)
View SolutionThe displacements of two interfering light waves are y_(1) = 2sin omega t and y_(2) = 5sin (omega t+(pi)/(3)) the resultant amptitude is
View SolutionTwo wave are represented by equation y_(1) = a sin omega t and y_(2) = a cos omega t the first wave :-
View SolutionTwo waves are represented by y_(1)= a sin (omega t + ( pi)/(6)) and y_(2) = a cos omega t . What will be their resultant amplitude
View SolutionThe equations for displacement of two light waves forming interference pattern are y_(1) = 4 sin omega t and y_(2) =3 sin (omega t+ (pi)/(2)) . Determine the amplitude of the resultant wave.
View SolutionEquations of two light waves are y1= 4 sin ω t and y2=3sin(ωt+π2). What is the amplitude of the resultant wave as they superpose on each other?
View SolutionThe displacement of two interfering light waves are given by y1=3sinωt,y2=4sin(ωt+π/2). The amplitude of the resultant wave is
View Solutiony1=asinωt और y2=bcosωt द्वारा निरूपित दो तरंगों में कलान्तर है :
View SolutionWhen the waves y_(1) = A sin omega t and y_(2) = A cos omega t are superposed, then resultant amplitude will be
View Solution
