A metal rod of resistance 20Ω is fixed along a diameter of a conducting ring of radius 0.1m and lies on x-y plane. There is a magnetic field →B=(50T)ˆk . The ring rotates with an angular velocity ω = 20rad /s about its axis. An external resistance of 10Ω is connected across the centre of the ring and rim. The current through external resistance is
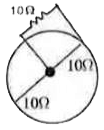
e=12Bl2ω=12×50×0.1×0.1×20
∴e=5V
Hence the current through the external resistance is
i=eR∴i=515=13amp
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IA
33 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IB
18 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
32 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
20 Videos
Similar Questions
A metal rod of resistance 20Ω is fixed along a diameter of a conducting ring of radius 0.1m and lies on x−y plane. There is a magnetic field →B=(50T)→k. The ring rotates with an angular velocity ω=20rads−1 about its axis. An external resistance of 10Ω is connected across the center of the ring and rim. The current external resistance is
View SolutionA metal rod of resistance R is fixed along a diameter of a conducting ring of radius r. There is a magnetic field of magnitude B perpendicular to the plane of the loop. The ring spins with an angular velocity ω about its axis. The centre of the ring is joined to its rim by an external wire W. The ring and W have no resistance. The current in W is
View Solution
Knowledge Check
A metal rod of resistance 20Ω is fixed along a diameter of a conducting ring of radius 0.1m and lies on x−y plane. There is a magnetic field →B=(50T)→k. The ring rotates with an angular velocity ω=20rads−1 about its axis. An external resistance of 10Ω is connected across the center of the ring and rim. The current external resistance is
A(a) 14B(b) 12C( c) 13D(d) 0A metal rod of resistance R is fixed along a diameter o fa conducting ring of radius r . There is a magnetic field of magnitude B perpendicular to the plane of the loop. The ring spins with an angular velocity ω about its axis. The centre of the ring is joined to its rim by an external wire W . The ring and W have no resistance. The current in W is
AzeroBBr2ω2RCBr2ωRD2Br2ωRA conducting ring of radius R has charge Q distributed unevenly over it. If it rotates with an angular velocity ω, the equivalent current will be
AzeroBQωCQω2πDQω2πR
A conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA charge Q is spread uniformly over an insulated ring of radius R.What is the magnetic moment of the ring if it is rotated with an angluar velocity ω about its axis?
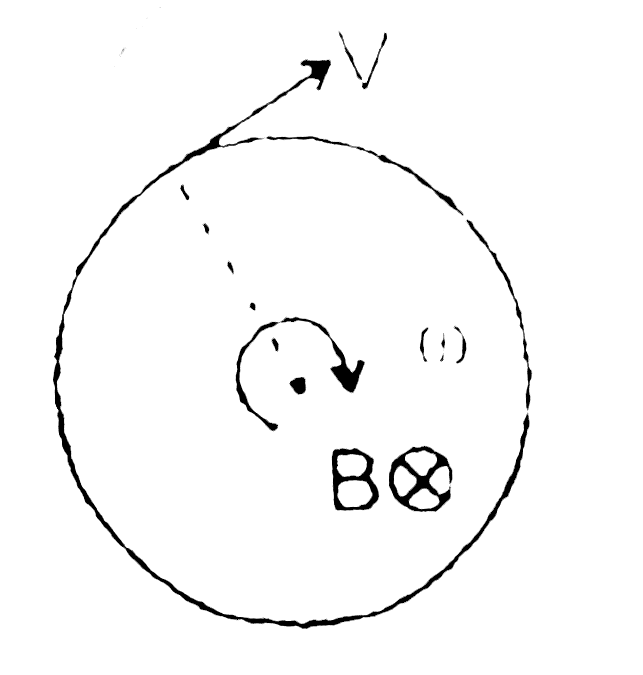
View SolutionA ring rotates with angular velocity ω about an axis perpendicular to the plane of the ring passing through the center of the ring.A constant magnetic field B exists parallel to the axis.Find the emf induced in the ring.
View Solution
