A metal rod of resistance is fixed along a diameter of a conducting ring of radius and lies on plane. There is a magnetic field . The ring rotates with an angular velocity about its axis. An external resistance of is connected across the center of the ring and rim. The current external resistance is
ZERO
The correct Answer is:C
To find the current in the external resistance connected across the conducting ring, we can follow these steps:
Step 1: Calculate the induced EMF (Electromotive Force)
The induced EMF (E) in the rotating ring can be calculated using the formula:
E=12Bωr2
Where:
- B=50T (magnetic field)
- ω=20rad/s (angular velocity)
- r=0.1m (radius of the ring)
Substituting the values:
E=12×50×20×(0.1)2
E=12×50×20×0.01
E=12×50×20×0.01=500100=5V
Step 2: Analyze the circuit configuration
The metal rod of resistance 20Ω is fixed along the diameter of the ring. This means that the rod can be considered as two resistors of 10Ω each in parallel since the total resistance is 20Ω.
Step 3: Determine the equivalent resistance of the rod
Since the two halves of the rod are in parallel:
Req=R1×R2R1+R2=10×1010+10=10020=5Ω
Step 4: Total resistance in the circuit
The total resistance in the circuit will be the sum of the equivalent resistance of the rod and the external resistance:
Rtotal=Req+Rexternal=5Ω+10Ω=15Ω
Step 5: Calculate the total current in the circuit
Using Ohm's law, the current I can be calculated as:
I=ERtotal=5V15Ω=13A
Final Answer
The current in the external resistance is:
I=13A
---
The induced EMF (E) in the rotating ring can be calculated using the formula:
E=12Bωr2
Where:
- B=50T (magnetic field)
- ω=20rad/s (angular velocity)
- r=0.1m (radius of the ring)
E=12×50×20×(0.1)2
E=12×50×20×0.01
E=12×50×20×0.01=500100=5V
The metal rod of resistance 20Ω is fixed along the diameter of the ring. This means that the rod can be considered as two resistors of 10Ω each in parallel since the total resistance is 20Ω.
Since the two halves of the rod are in parallel:
Req=R1×R2R1+R2=10×1010+10=10020=5Ω
The total resistance in the circuit will be the sum of the equivalent resistance of the rod and the external resistance:
Rtotal=Req+Rexternal=5Ω+10Ω=15Ω
Using Ohm's law, the current I can be calculated as:
I=ERtotal=5V15Ω=13A
The current in the external resistance is:
I=13A
Similar Questions
A metal rod of resistance R is fixed along a diameter of a conducting ring of radius r. There is a magnetic field of magnitude B perpendicular to the plane of the loop. The ring spins with an angular velocity ω about its axis. The centre of the ring is joined to its rim by an external wire W. The ring and W have no resistance. The current in W is
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA ring rotates with angular velocity ω about an axis perpendicular to the plane of the ring passing through the center of the ring.A constant magnetic field B exists parallel to the axis.Find the emf induced in the ring.

View SolutionA ring of radius 0.5 m and mass 10 kg is rotating about its diameter with angular velocity of 20rads−1. Its kinetic energy is
View SolutionA ring rotates with angular velocity ω about an axis perpendicula to the plane of the ring passing through the center of the ring (Fig. 3.77). A constant magnetic field B exists parallel to the axis. Find the emf induced in the ring.

View SolutionAB is a resistanceless conducting rod which forms a diameter of a conducting ring of radius r rotating in a uniform magnetic field B as shown in figure. The resistance R1 and R2 do not rotate. Then the current through the resistor R1 is
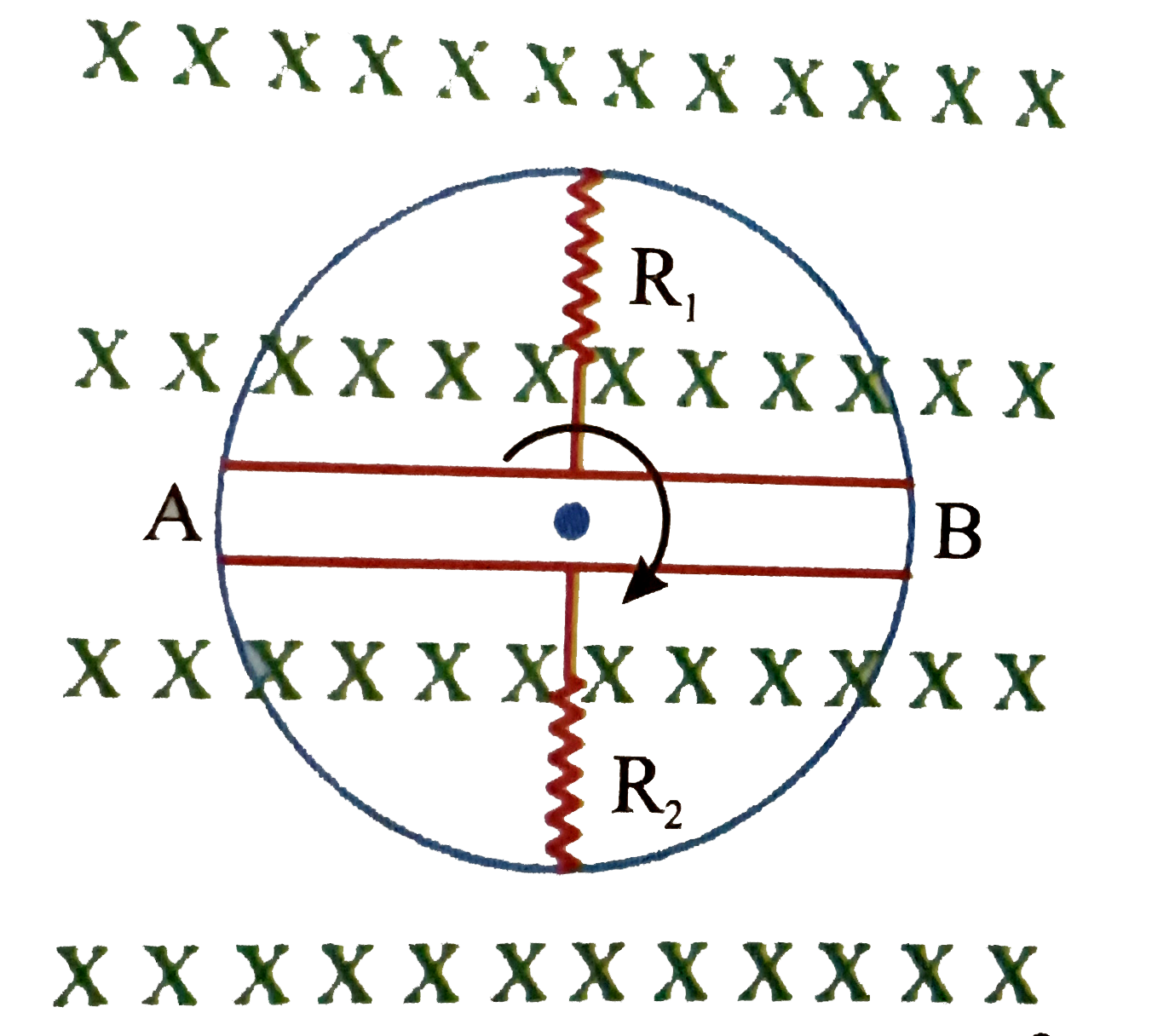
View SolutionAB is a resistanceless conducting rod which forms a diameter of a conducting ring of radius r rotating in a uniform magnetic field B as shown in figure. The resistance R1 and R2 do not rotate. Then the current through the resistor R1 is

View SolutionA ring of mass m and radius r is rotated in uniform magnetic field B which is perpendicular to the plane of the loop with constant angular velocity ω0.Find the net ampere force on the ring and the tension developed in the ring if there is a current i in the ring.Current and rotation both are clockwise.

View SolutionA metal disc of radius R=25cm rotates with a constant angular velocity ω=130 rad s−1 about its axis. Find the potential difference between the center and rim of the disc if
(a) the external magnetic field is absent,
(b) the external uniform magnetic field B=5.0mT directed perpendicular to the disc.
View Solution
