A uniform rod o length one meter is bent at its midpoint to make 90∘. The distance of centre of mass from the centre of rod is (in cm)
20.2
13.4
15
17.6
The correct Answer is:D
To find the distance of the center of mass from the center of a bent uniform rod, we can follow these steps:
Step 1: Understand the Configuration
The rod is 1 meter long and is bent at its midpoint to form a right angle (90 degrees). This means that each segment of the rod is 0.5 meters long.
Step 2: Identify the Center of Mass of Each Segment
Since the rod is uniform, the center of mass of each straight segment (0.5 meters long) will be at its midpoint. Therefore, the center of mass of each segment is located at 0.25 meters from the bend (the midpoint).
Step 3: Set Up the Coordinate System
Let’s place the bend at the origin (0,0) of a coordinate system:
- The first segment (horizontal) extends from (-0.25, 0) to (0.25, 0).
- The second segment (vertical) extends from (0, -0.25) to (0, 0.25).
Step 4: Calculate the Center of Mass
The coordinates of the center of mass for each segment can be calculated as follows:
- For the horizontal segment:
(x1,y1)=(0.25,0)
- For the vertical segment:
(x2,y2)=(0,−0.25)
Step 5: Use the Center of Mass Formula
The center of mass (CM) of the entire system can be calculated using the formula:
xCM=m1x1+m2x2m1+m2
yCM=m1y1+m2y2m1+m2
Since the rod is uniform, we can assume m1=m2=m (mass of each segment is equal):
xCM=m(0.25)+m(0)m+m=0.25m2m=0.125 m
yCM=m(0)+m(−0.25)m+m=−0.25m2m=−0.125 m
Step 6: Calculate the Distance from the Center of the Rod
The center of the rod is at (0,0). The distance from the center of mass to the center of the rod can be calculated using the distance formula:
d=√(xCM−0)2+(yCM−0)2=√(0.125)2+(−0.125)2
d=√0.015625+0.015625=√0.03125=0.176776695 m
Step 7: Convert to Centimeters
To convert meters to centimeters, we multiply by 100:
d=0.176776695×100=17.6776695 cm≈17.68 cm
Final Answer
The distance of the center of mass from the center of the rod is approximately 17.68 cm.
---
The rod is 1 meter long and is bent at its midpoint to form a right angle (90 degrees). This means that each segment of the rod is 0.5 meters long.
Since the rod is uniform, the center of mass of each straight segment (0.5 meters long) will be at its midpoint. Therefore, the center of mass of each segment is located at 0.25 meters from the bend (the midpoint).
Let’s place the bend at the origin (0,0) of a coordinate system:
- The first segment (horizontal) extends from (-0.25, 0) to (0.25, 0).
- The second segment (vertical) extends from (0, -0.25) to (0, 0.25).
The coordinates of the center of mass for each segment can be calculated as follows:
- For the horizontal segment:
(x1,y1)=(0.25,0)
- For the vertical segment:
(x2,y2)=(0,−0.25)
The center of mass (CM) of the entire system can be calculated using the formula:
xCM=m1x1+m2x2m1+m2
yCM=m1y1+m2y2m1+m2
Since the rod is uniform, we can assume m1=m2=m (mass of each segment is equal):
xCM=m(0.25)+m(0)m+m=0.25m2m=0.125 m
yCM=m(0)+m(−0.25)m+m=−0.25m2m=−0.125 m
The center of the rod is at (0,0). The distance from the center of mass to the center of the rod can be calculated using the distance formula:
d=√(xCM−0)2+(yCM−0)2=√(0.125)2+(−0.125)2
d=√0.015625+0.015625=√0.03125=0.176776695 m
To convert meters to centimeters, we multiply by 100:
d=0.176776695×100=17.6776695 cm≈17.68 cm
The distance of the center of mass from the center of the rod is approximately 17.68 cm.
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -II(H.W)
Explore 47 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-V
Explore 72 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:NCERT based questions
Explore 15 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
Imagine a hole drilled along the radius of the earth. A uniform rod of length equal to the radius (R) of the earth is inserted into this hole. Find the distance of centre of gravity f the rod from the centre .

View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View Solution
Knowledge Check
A thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is
 AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)
AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)A uniform wire of length l is bent into the shape of 'V' as shown. The distance of its centre of mass from the vertex A is :-
 Al/2Bl√34Cl√38DNone of these
Al/2Bl√34Cl√38DNone of theseA uniform metre rod is bent into L shape with the bent arms at 90∘ to each other. The distance of the centre of mass from the bent point is
AL4√2mBL2√2mCL√2mDL8√2m
A uniform thin rod of length 3L is bent at right angles at a distance L from one end as shown in Fig. If length of rod is 1.8m, find the co-ordinates and position vector of the mass of the system.

View SolutionA uniform rod of length l is given an impulse at right angles to its length as shown. Find the distance of instantaneous centre of rotation from the centre of the rod.
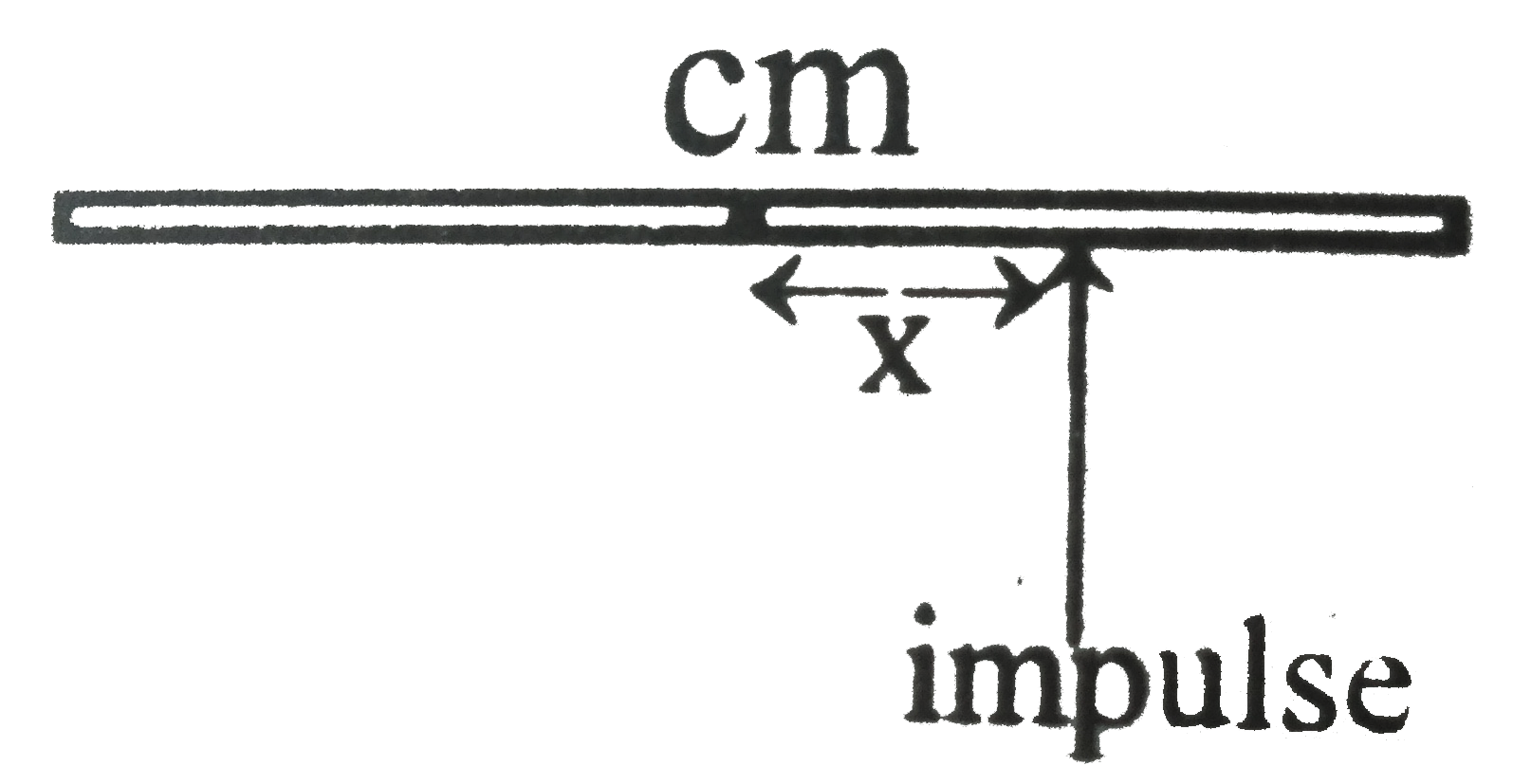 .
.
View SolutionThe mass per unit length of a non- uniform rod OP of length L varies as m=k(x)/(L) where k is a constant and x is the distance of any point on the rod from end 0 .The distance of the centre of mass of the rod from end 0 is
View SolutionTwo identical thin uniform rods of length L each are joined to form T shape as shown in the figure. The distance of centre of mass from D is
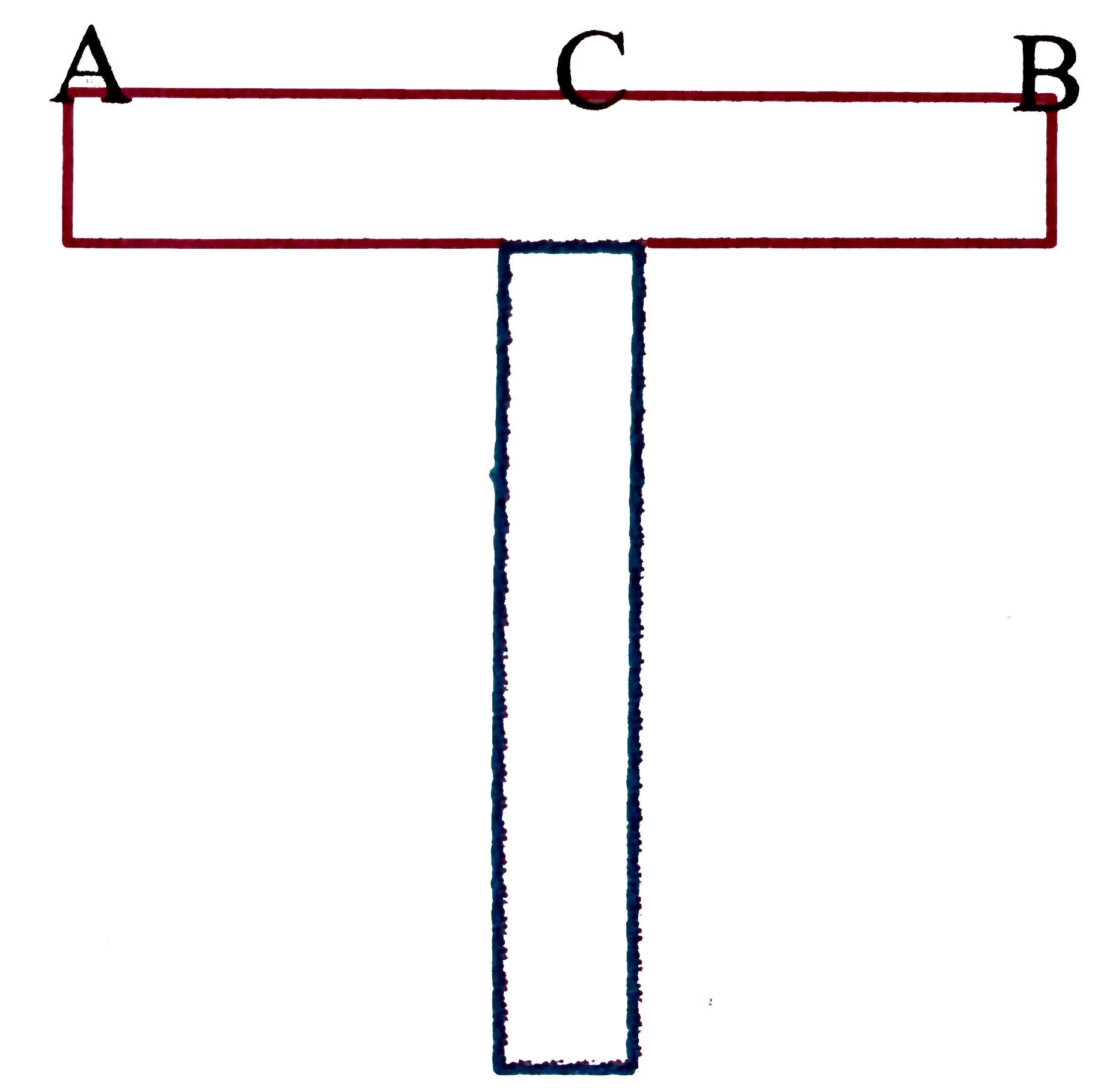
View SolutionA uniform metal rod of length 1m is bent at 90∘, so as to form two arms of equal length. The centre of mass of this bent rod is
View Solution
