A charge q of mass m enters a region of electric field with a velocity at origin. Find the x coordinate where the charge hits the x axis again. (Neglect effect of gravity)
The correct Answer is:B
To solve the problem, we need to analyze the motion of the charged particle in the electric field. Here's a step-by-step breakdown of the solution:
Step 1: Understanding the Initial Conditions
The charge q of mass m enters the electric field at the origin with an initial velocity given by:
→v0=v0^i+v0^j
This means that the charge has equal components of velocity in both the x and y directions.
Step 2: Analyzing the Electric Field
The electric field is given by:
→E=−E0^j
This indicates that the electric field is directed downward (in the negative y-direction). The force on the charge due to the electric field is given by:
→F=q→E=−qE0^j
This force will cause an acceleration in the negative y-direction.
Step 3: Finding the Acceleration
Using Newton's second law, the acceleration →a of the charge can be calculated as:
→a=→Fm=−qE0m^j
This shows that the charge experiences a constant acceleration downward.
Step 4: Motion in the x-direction
In the x-direction, there is no force acting on the charge, so it moves with a constant velocity. The x-component of the velocity remains:
vx=v0
The x-coordinate as a function of time t is given by:
x(t)=v0t
Step 5: Motion in the y-direction
In the y-direction, the charge is subject to constant acceleration. The equation of motion for the y-coordinate y(t) is:
y(t)=v0yt+12ayt2
Where v0y=v0 and ay=−qE0m. Thus, we can write:
y(t)=v0t−12qE0mt2
Step 6: Finding the Time to Hit the x-axis
The charge hits the x-axis when y(t)=0:
0=v0t−12qE0mt2
Factoring out t:
t(v0−12qE0mt)=0
This gives two solutions: t=0 (the initial time) and:
t=2v0mqE0
Step 7: Finding the x-coordinate at this time
Substituting t back into the equation for x(t):
x(2v0mqE0)=v0(2v0mqE0)=2v20mqE0
Final Result
Thus, the x-coordinate where the charge hits the x-axis again is:
2v20mqE0
The charge q of mass m enters the electric field at the origin with an initial velocity given by:
→v0=v0^i+v0^j
This means that the charge has equal components of velocity in both the x and y directions.
The electric field is given by:
→E=−E0^j
This indicates that the electric field is directed downward (in the negative y-direction). The force on the charge due to the electric field is given by:
→F=q→E=−qE0^j
This force will cause an acceleration in the negative y-direction.
Using Newton's second law, the acceleration →a of the charge can be calculated as:
→a=→Fm=−qE0m^j
This shows that the charge experiences a constant acceleration downward.
In the x-direction, there is no force acting on the charge, so it moves with a constant velocity. The x-component of the velocity remains:
vx=v0
The x-coordinate as a function of time t is given by:
x(t)=v0t
In the y-direction, the charge is subject to constant acceleration. The equation of motion for the y-coordinate y(t) is:
y(t)=v0yt+12ayt2
Where v0y=v0 and ay=−qE0m. Thus, we can write:
y(t)=v0t−12qE0mt2
The charge hits the x-axis when y(t)=0:
0=v0t−12qE0mt2
Factoring out t:
t(v0−12qE0mt)=0
This gives two solutions: t=0 (the initial time) and:
t=2v0mqE0
Substituting t back into the equation for x(t):
x(2v0mqE0)=v0(2v0mqE0)=2v20mqE0
Thus, the x-coordinate where the charge hits the x-axis again is:
2v20mqE0
Similar Questions
The space has electromagnetic field which is given as →B=−B0ˆk and →E=E0ˆk. A charged particle having mass m and positive charge q is given velocity v0ˆi at origin at t=0sec. The z coordinate of the particle when it passes through the z−axis is (neglect gravity through motion)
View SolutionA proton of charge e and mass m enters a uniform magnetic field B=Bi with an initial velocity v=vxˆi+vyˆj. Find an expression in unit vector notation for its velocity at time t.
View Solution
Knowledge Check
A particle of charge q and mass m enters a region of a transverse electric field of E0ˆj with initial velocity v0ˆi . The time taken for the change in the de Broglie wavelength of the charge from the initial value of λ0 to λ0/3 is proportional to
AqmBmqC√qmD√mqElectric field strength →E=E0ˆi and →B=B0ˆi exists in a region. A charge is projected with a velocity →v=v0ˆj origin, then
AIt moves along helix with constant pitchBIt moves along circular path in Y Z planeCIt moves along helix with increasing pitchDIt moves along helix with decreasing pitchAssertion: A charged particle enters in a magnetic field B=B0ˆiwithvelocityv=v0ˆi+v0ˆj, then minimum speed of charged particle may be v0.
Reason: A variable acceleration particle may be v0.AIf both Assertion and Reason are true and the Reason is correct explanation of the Assertion.BIf both Assertion and Reason are true but Reason is not the correct explanation of AssertionCIf Assertion is true, but the Reason is false.DIf Assertion is false but the Reason is true.
A particle of specific charge alpha enters a uniform magnetic field B=−B0ˆk with velocity v=v0ˆi from the origin. Find the time dependence of velocity and position of the particle.

View SolutionA particle having mass m and charge q is released from the origin in a region in which electric field and magnetic field are ginen by
B=+B0ˆj and →E=+E0ˆi.
Find the speed of the particle as a function of its X-coordinate.
View SolutionThe diagram shows combination of three cuboidal spaces (1),(2) and (3). Space 1 and 3 contain electric field E as shown while space 2 has magnetic field B. A particle of charge q and mass m is projected as shown with velocity V0cosθ(i)+V0sinθˆj. Find the value of E, so that his particle enters the magnetic field parallel to the x-axis and just passes through point P along the electric field at that point. Find its speed at P and also the ratio L/R (Neglect the effect of gravity)
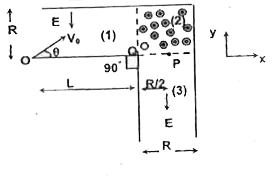
View SolutionA particle having mass m and charge q is released from the origin in a region in which electric field and megnetic field are given by →B=−B0ˆj and →E=→E0ˆk. Find the speed of the particle as a function of its z-coordinate.
View SolutionA positive charge particle to charge q& mass m is released at origin.There are unifrom magnetic and electric field in the space given by →E=E0ˆj&→B=B0ˆk, where E0&B0 are constants.Find the y coordinate of the particle at time t.
View Solution