A metallic wire of density d floats horizontal in water. The maximum radius of the wire so that the wire may not sink is (surface tension of water = T)
√2Tπdg
√2πTdg
√2πTgd
√2πTgd
The correct Answer is:A
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDS BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-IB (ASSERTION & REASON)
46 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-2
68 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-3
43 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
108 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE - 3
26 Videos
Similar Questions
A metallic wire of diameter d is lying horizontally on the surface of water. The maximum length of wire so that it may not sink will be
View SolutionA wire of mass 1g is kept horizontally on the surface of water. The length of the wire that does not break the surface film is (surface tension of water is 70dy≠cm−1)
View Solution
Knowledge Check
A metalic wire of diameter d is lying horizontally o the surface of water. The maximum length of wire so that is may not sink will be
A√2TπdgB√2TgπdC√2πdTgDany lengthA wire of length l metre made of a material of specific gravity 8 is floating horizontally on the surface of water if it is not wet by water the maximum diameter of the wire upto which it can continue to float is (surface tension of water is T=70xx10^-3Nm^-1)
A1.5B1.1C0.75D0.55A wire of length l metre made of a material of specific gravity 8 is floating horizontally on the surface of water if it is not wet by water the maximum diameter of the wire upto which it can continue to float is (surface tension of water is T=70xx10^-3Nm^-1)
A1.5B1.1C0.75D0.55
A metal wire of density ρ floats on water surface horozontally. If is NOT to sink in water, then maximum radius of wire is proportional to (where, T=surface tension of water, g=gravitational acceleration)
View SolutionA wire of length L metres, made of a material of specific gravity 8 is floating horizontally on the surface of water. If it is not wet by water, the maximum diameter of the wire (in mm) upto which it can continue to float is (surface tension of water is T=70×10−3Nm−1)
View SolutionA wire of mass 1g is kept horizontally on the surface of water. The length of the wire that does not break the surface film is (surface tension of water is 70dy≠cm−1)
View SolutionA metal wire of density ρ floats on water surface horozontally. If is NOT to sink in water, then maximum radius of wire is proportional to (where, T=surface tension of water, g=gravitational acceleration)
View SolutionTwo blocks of masses m and 2m are connected through a wire fo breakig stress S passing over a frictionless pulley. The maximum radius of the wire to be used so that the wire may not break is
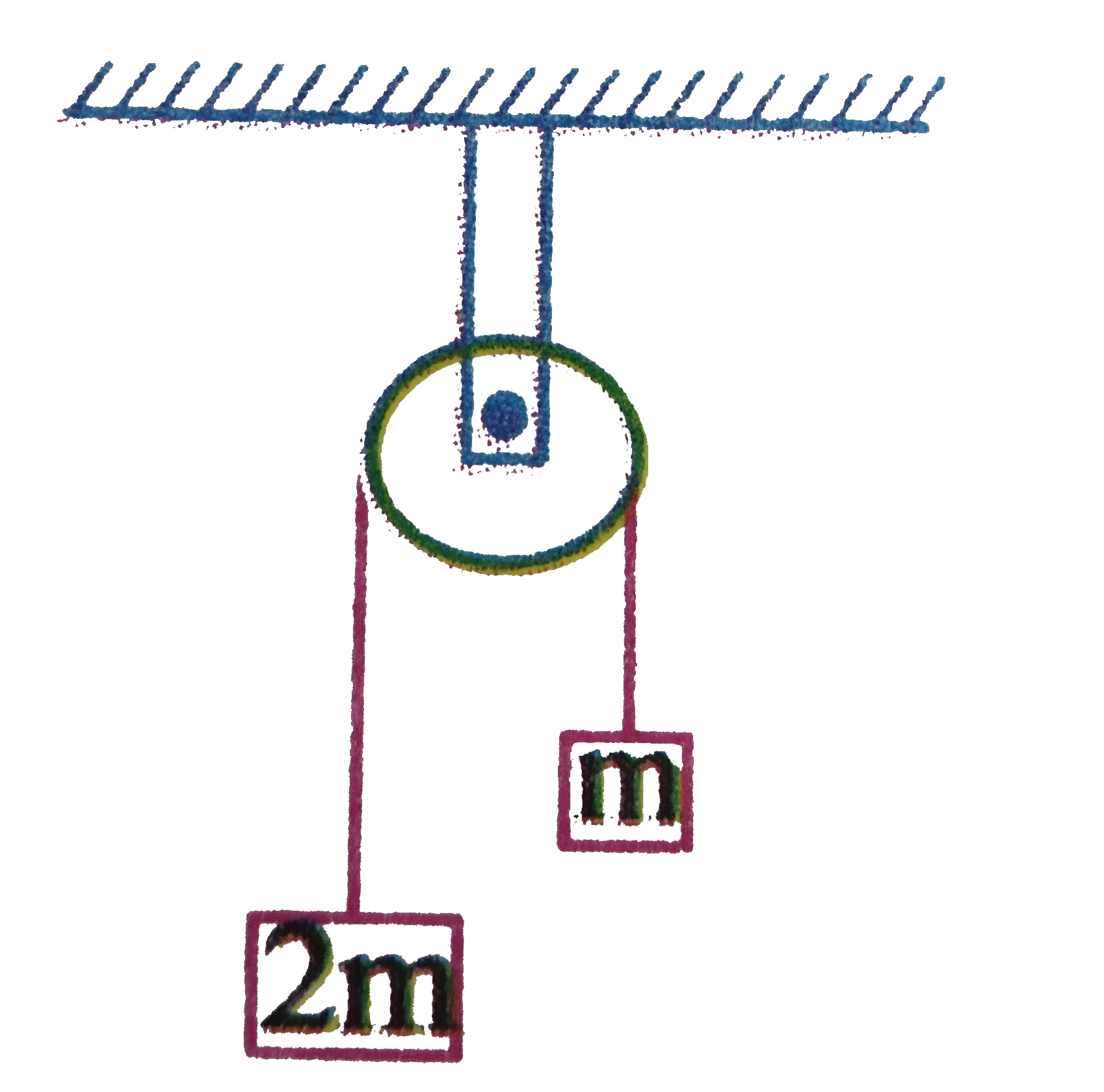
View Solution
