The ends of an well-lagged copper bar of length L are held at steady temperature θ1andθ2(θ1>θ2)
Which graph best represents the relationship between dQ/dt, the rate of flow of heat, and x, the distance from the hot end when all temperatures in the bar are steady ?
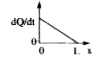
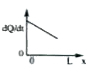
The correct Answer is:D
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE-IB68videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE-2106videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions2videos
THERMAL PROPERTIES OF MATTER
- BOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE99videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 333videos
THERMODYNAMICS
Similar Questions
The ends of a metal rod are kept at temperature θ1andθ2 with θ2>θ1. At steady state the rate of flow of heat along the rod is directly proportional to
View SolutionThe ends of a metal rod are kept at temperatures θ1 and θ2 with θ2>θ1. The rate of flow of heat along the rod is directly proportional to
View Solution
Knowledge Check
- Question 1 - Select One
A metal bar of length l is well lagged with some non-conducting material to prevent losses of heat from its surface and the two ends are maintained at steady temperatures θ1 and θ2 with θ1>θ2, then in the steady state the temperature θ of s section of the bar at distance x from the hot end varies as shown in the graph
A
B
C
D
- Question 2 - Select One or More
The ends of a metal rod are kept at temperature θ1andθ2 with θ2>θ1. At steady state the rate of flow of heat along the rod is directly proportional to
Athe length of the rodBthe diameter of the rodCthe cross-sectional area of the rodDthe temperature difference (θ2−θ1) between the ends of the rod - Question 3 - Select One or More
The ends of a metal rod are kept at temperatures θ1 and θ2 with θ2>θ1. The rate of flow of heat along the rod is directly proportional to
Athe length of the rodBthe diameter of the rodCthe cross sectional area of the rodDthe temperature difference (θ2−θ1) between the ends of the rod
The two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
View SolutionTwo different metal rods of the same length have their ends kept at the same temperature θ1, and θ2with θ2>θ1. If A1 and A2 are their cross-sectional areas and K1 and K2 their thermal conductivities, the rate of flow of heat in the two rods will be the same it:
View SolutionThe two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
View SolutionThe rate of flow of heat through a metal bar of area of cross-section 1 m2 when temperature gradient is 1∘C/m under steady state is called
View SolutionThe ends of a metal bar of constant cross-sectional area are maintained at temperatures T1andT2 which are both higher than the temperature of the surroundings. If the bar is unlagged, which one of the following sketches best represents the variation of temperature with distance along the bar ?
View Solution