The two ends of a rod of length and a uniform cross-sectional area are kept at two temperature and . The rate of heat transfer. , through the rod in a steady state is given by
The correct Answer is:d
To solve the problem of determining the rate of heat transfer through a rod with given temperatures at its ends, we can follow these steps:
1. Understand the Setup:
- We have a rod of length L and uniform cross-sectional area A.
- One end of the rod is at temperature T1 and the other end is at temperature T2 with T1>T2.
2. Identify the Heat Transfer Mechanism:
- Heat transfer through the rod occurs due to conduction, which is governed by Fourier's law of heat conduction.
3. Apply Fourier's Law:
- According to Fourier's law, the rate of heat transfer dQdt through a material is proportional to the temperature difference across it and the area through which heat is being transferred, and inversely proportional to the length of the rod.
- The formula is given by:
dQdt=k⋅A⋅(T1−T2)L
- Here, k is the thermal conductivity of the material of the rod.
4. Substitute the Known Values:
- Since T1>T2, the temperature difference (T1−T2) is positive, which indicates that heat flows from the higher temperature end to the lower temperature end.
5. Final Expression:
- Thus, the rate of heat transfer through the rod can be expressed as:
dQdt=k⋅A⋅(T1−T2)L
Final Answer:
dQdt=k⋅A⋅(T1−T2)L
- We have a rod of length L and uniform cross-sectional area A.
- One end of the rod is at temperature T1 and the other end is at temperature T2 with T1>T2.
- Heat transfer through the rod occurs due to conduction, which is governed by Fourier's law of heat conduction.
- According to Fourier's law, the rate of heat transfer dQdt through a material is proportional to the temperature difference across it and the area through which heat is being transferred, and inversely proportional to the length of the rod.
- The formula is given by:
dQdt=k⋅A⋅(T1−T2)L
- Here, k is the thermal conductivity of the material of the rod.
- Since T1>T2, the temperature difference (T1−T2) is positive, which indicates that heat flows from the higher temperature end to the lower temperature end.
- Thus, the rate of heat transfer through the rod can be expressed as:
dQdt=k⋅A⋅(T1−T2)L
dQdt=k⋅A⋅(T1−T2)L
Similar Questions
Two ends of a rod of non uniform area of cross section are maintained at temperature T1and T2 (T1>T2) as shown in the figure
If l is heat current through the cross-section of conductor at distance x from its left face, then the variation of l with x is best represented by
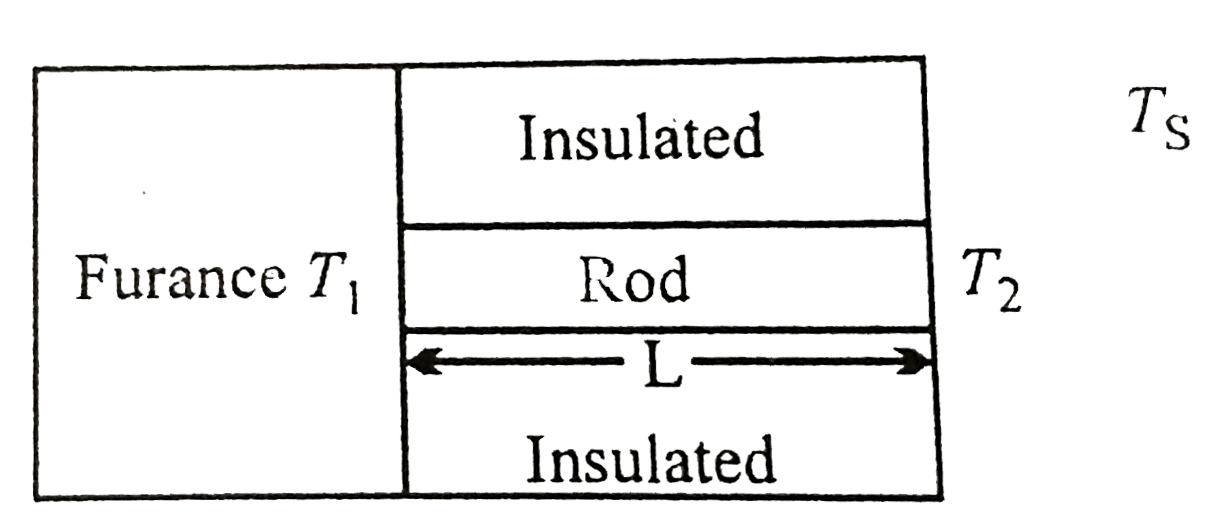
View SolutionOne end of a rod of length L and crosssectional area A is kept in a furnace at temperature T1. The other end of the rod is kept at a temperature T2. The thermal conductivity of the matrieal of the rod is K and emissivity of the rod is e. It is gives that T!=Ts+ΔT, where ΔT<<Ts,Ts is the temperature of the surroundings. If ΔT∝(T1−T2) find the proportional constant, consider that heat is lost only by rediation at the end where the temperature of the rod is T1.

View Solution
Knowledge Check
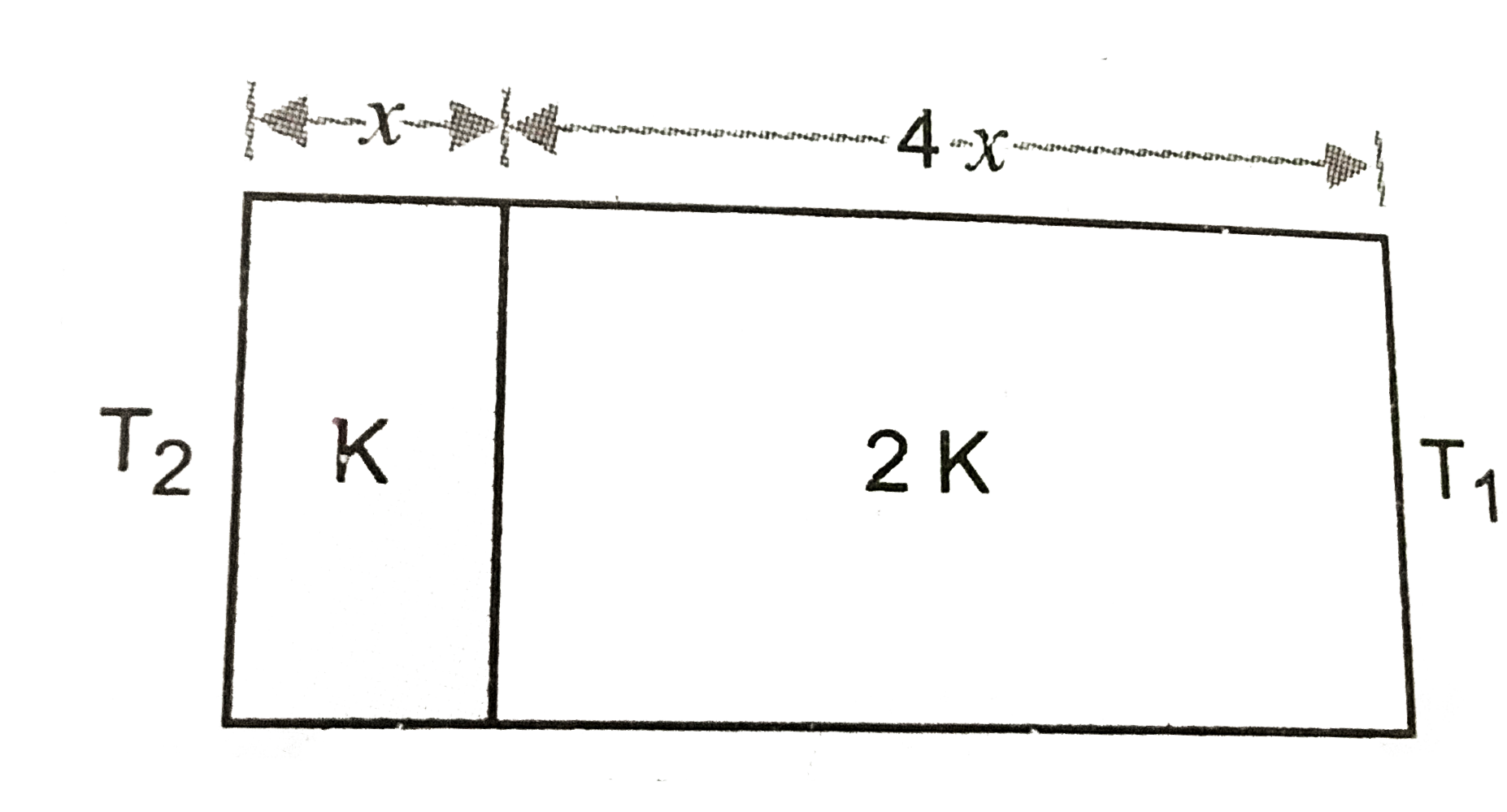
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x respectively. Temperatures on the opposite faces of composite slab are T1andT2 where T2>T1, as shown in fig. what is the rate of flow of heat through the slab in a steady state?
 A1B12C23D13
A1B12C23D13
One end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
View SolutionThree rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.

View Solution
Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod is
View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thicknesses x and 4x, respectively are T2 and T1(T2>T1). The rate of heat of heat transfer through the slab, in ? steady state is [(AT2−T1x]f, with f equal to :-

View SolutionThe ends of a metal rod are kept at temperature θ1andθ2 with θ2>θ1. At steady state the rate of flow of heat along the rod is directly proportional to
View SolutionThe temperature of the two outer surfaces of a composite slab consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab in steady state is (AK(T2−T1)x)f. where, f is equal to
 .
.
View SolutionThree rods of the same length and the same area of the cross-section are joined. The temperature of two ends one T1 and T2 as shown in the figure.
 As we move along the rod the variation of temperature are as shown in the following [Rods are insulated from the surrounding except at the faces]
As we move along the rod the variation of temperature are as shown in the following [Rods are insulated from the surrounding except at the faces]

View Solution
