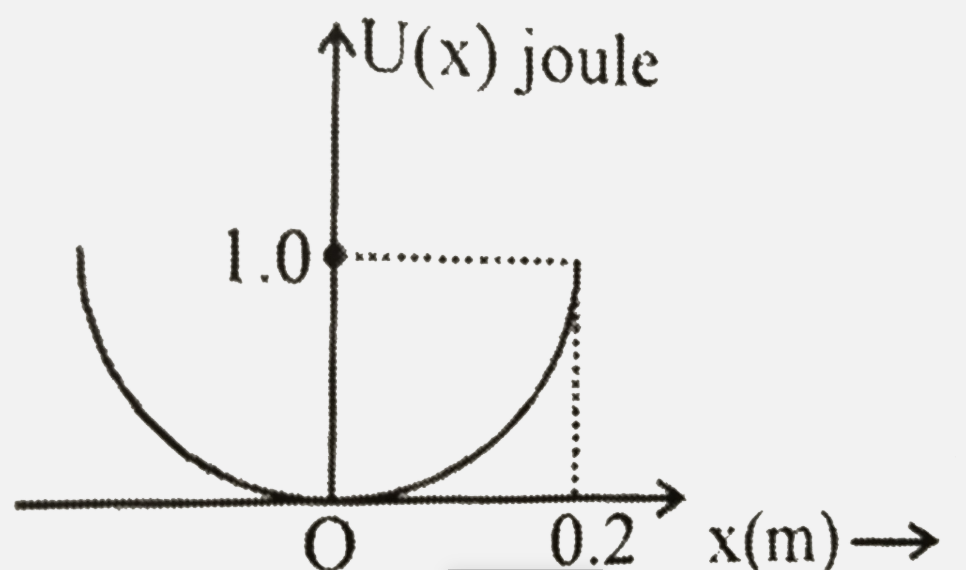
The variation of PE of a simple harmonic oscillator is as shown. Then force constant of the system is (PE 'U' is in joules, displacement 'x' is in mm)
 Solution in Telugu
Solution in Telugu
100N/m
150N/m
2003N/m
300N/m
The correct Answer is:B
Step by step video & image solution for The variation of PE of a simple harmonic oscillator is as shown. Then force constant of the system is (PE 'U' is in joules, displacement 'x' is in mm) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - AAKASH SERIESCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II)(LECTURE SHEET (ADVANCED))(STRIGHT OBJECTIVE TYPE QUESTIONS)
7 Videos
- SIMPLE HARMONIC MOTION BOOK - AAKASH SERIESCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II)(PRACTICE SHEET (ADVANCED)) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
1 Videos
- SIMPLE HARMONIC MOTION BOOK - AAKASH SERIESCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - PRACTICE SHEET (EXERCISE - V)(LEVEL - II)(INTEGER TYPE QUESTIONS)
2 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
- SURFACE TENSIONBOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS )
8 Videos
Similar Questions
A particle of mass m is subjected to a force →F=F0[cos(t)ˆi+sin(t)ˆj]. If initially (t=0) the particle was at rest, the kinetic energy particle as a function of time is given by:
View SolutionFrequency of a particle executing SHM is 10Hz. The particle is suspended from a vertical spring.At the highest point of its oscillation the spring is unstretched. Maximum speed of the particle is (g=10m/s2)
View SolutionA particle is placed at the lowest point of a smooth parabola having the equation x2=5y( x,y are in metre). After a slight displacement, the particle is constrained to move along the parabola. Find the angular frequency of oscillations (in rad/sec).
View SolutionA wheel rotates with an angular acceleration given by α=4at2−3bt2, where t is the time and a and bare constants. If the wheel has an initial angular speed w0, write the equations for (a) the angular speed and (b) the angle tumed through as functions of time.
View SolutionIf the work done in blowing a soap bubble of volume 'V' is W, then the work done in blowing a soap bubble of volume '2V' is
View SolutionThe variation of potential energy (U) of a simple harmonic oscillator is as shown. Then force constant of the system is (PE is in joules, displacement 'x' is in mm)
View SolutionDraw a graph to show the variation of PE, KE and total energy of a simple harmonic oscillator with displacement.
View SolutionFind the displacement of a simple harmonic oscillator at which its PE is half of the maximum energy of the oscillator.
View SolutionA particle of mass 4kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillations is :-
View SolutionThe displacement of a particle of mass 1 kg in S.H.M. is x = 2 sin (pit+phi) m. Then variation of its PE in joule is
View SolutionAt what displacement (i) the PE and (ii) KE of a simple harmonic oscillator is maximum?
View SolutionDraw a graph to show the variation of PE, KE and total energy of a simple harmonic oscillator with displacement.
View SolutionFind the displacement of a simple harmonic oscillator at which its PE is half of the maximum energy of the oscillator.
View SolutionDraw a graph to show the variation of PE, KE and total energy of a simple harmonic oscillator with displacement.
View SolutionFind the displacement of a simple harmonic oscillator at which its PE is half of the maximum energy of the oscillator.
View Solution
