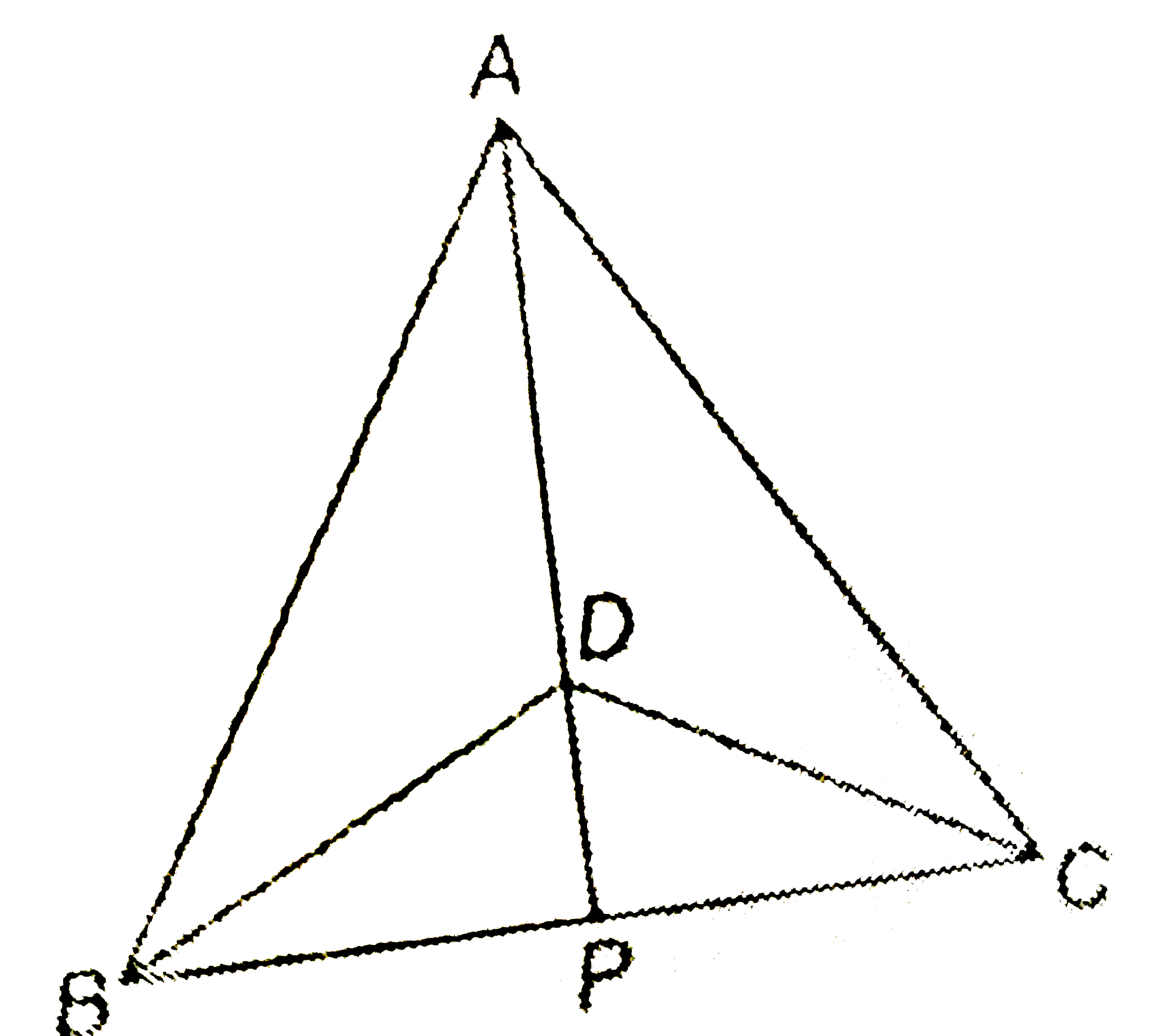
ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
The correct Answer is:CP
Step by step video & image solution for DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that : (i) DeltaABD cong DeltaACD (ii) DeltaABP cong DeltaACP (iii) AP bisects angleA as well as angleD (iv) AP is the perpendicular bisector of BC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.4
6 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.5
4 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.2
8 Videos
- SURFACE AREAS AND VOLUMESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS
18 Videos
Similar Questions
ΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that
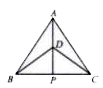
ΔABP≅ΔACP
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that
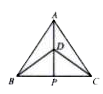
ΔABD≅ΔACD
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E show that
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that
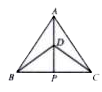
AP bisects ∠A as well as ∠D.
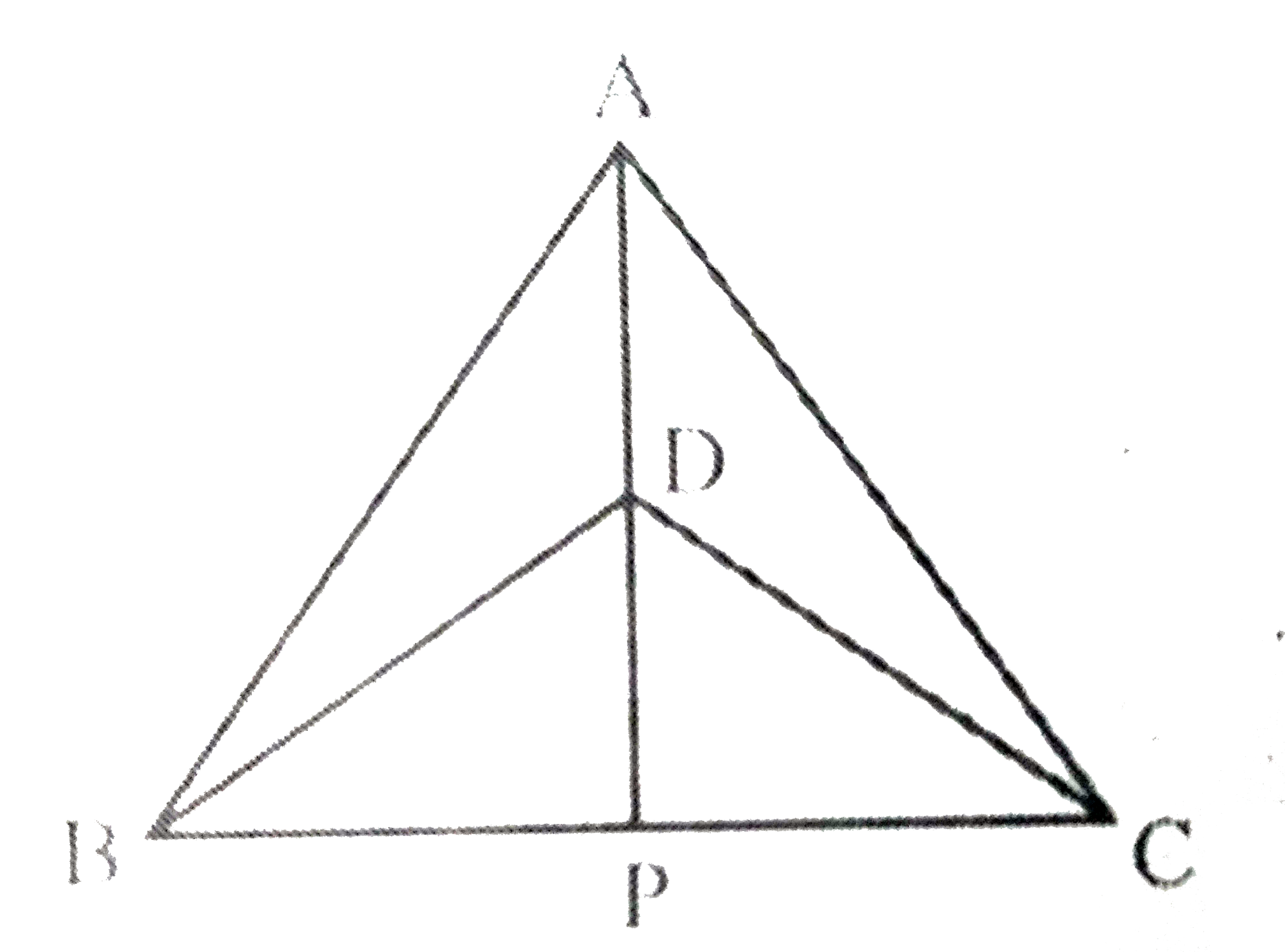
View SolutionΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC
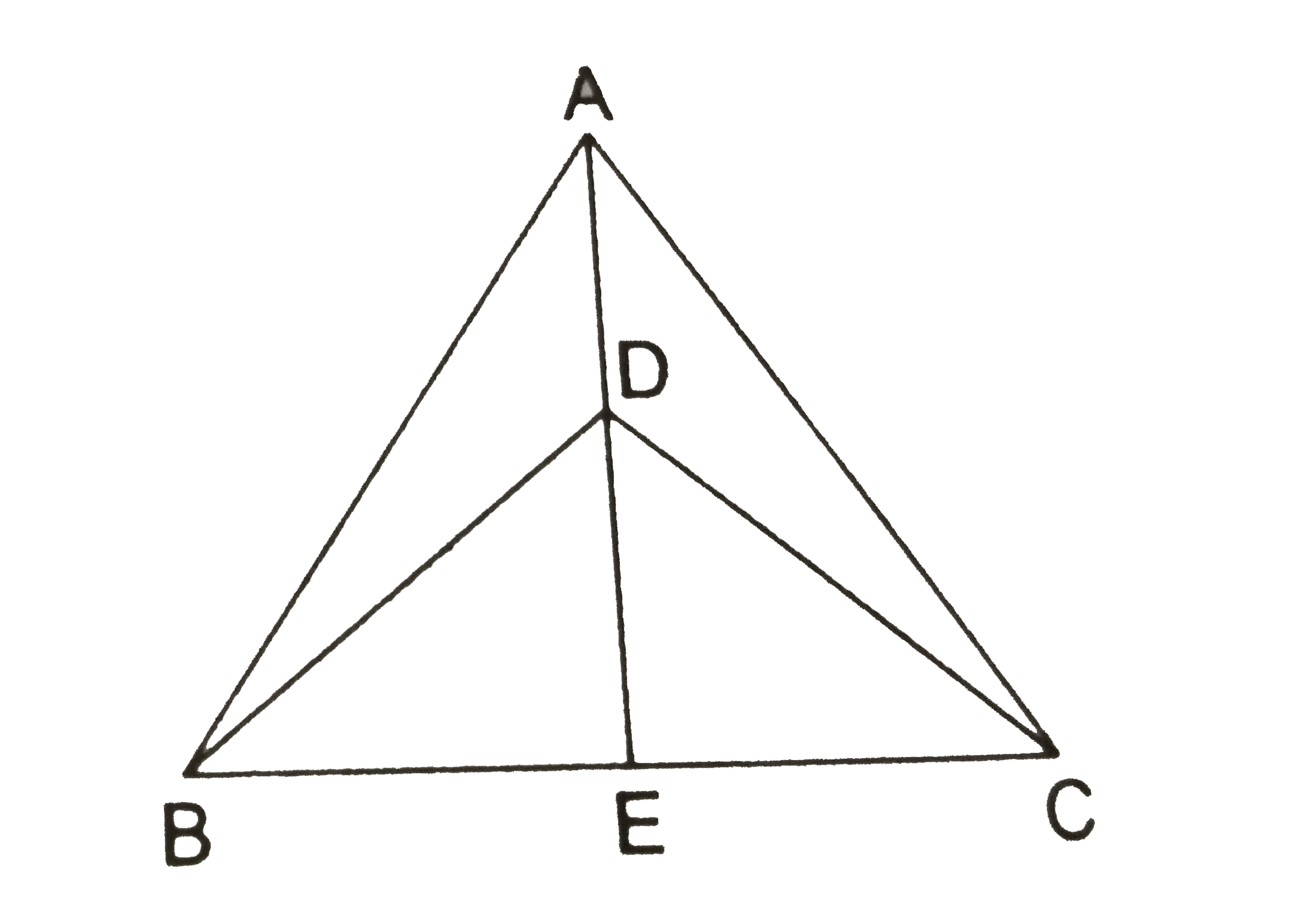
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E, show that
(i) ΔABD≅ΔACD
(ii) ΔABE≅ΔACE
(iii) AE bisects ∠A as well as ∠D
(iv) AE is the perpendicualr bisector of BC.
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD ≅ACD (ii) ABP ≅ACP
View Solution△ABC and △DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that (i) △ABD≅△ACD (ii) △ABP≅△ACP (iii) AP bisects ∠A as well as △D. (iv) AP is the perpendicular bisector of BC.
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that AP bisects \ ∠A as well as ∠D AP is the perpendicular bisector of BC
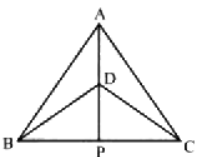
View SolutionABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD≅ACD (ii) ABP≅ACP AP bisects ∠A as well as ∠D AP is perpendicular bisector of BC.
View Solution
