AB is a diameter of a circle with centre O. CD is a chord equal to the radius of the circle. AC and BD are produced to meet at P. Then the measure of ∠APB is:
120∘
30∘
60∘
90∘
The correct Answer is:C
Similar Questions
AB is diameter of a circle with centre 'O'. CD is a chord which is equal to the radius of the circle. AC and BD are extended so that they intersect each other at point P. Then find the value of ∠APB.
View SolutionAB is a diameter of a circle with centre O. Chord CD is equal to radius OC. AC and BD produced intersect at P. Prove that : ∠APB=60∘
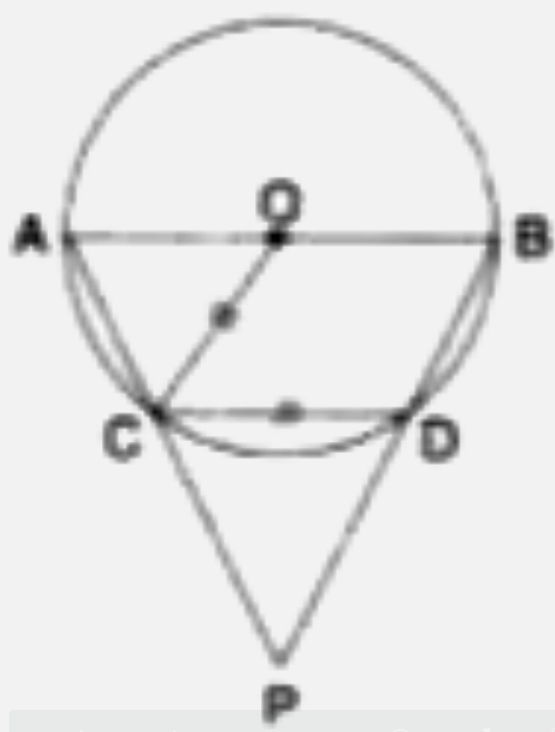
View Solution
Knowledge Check
AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Find the ∠AEB.
A30∘B60∘C90∘D45∘AB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
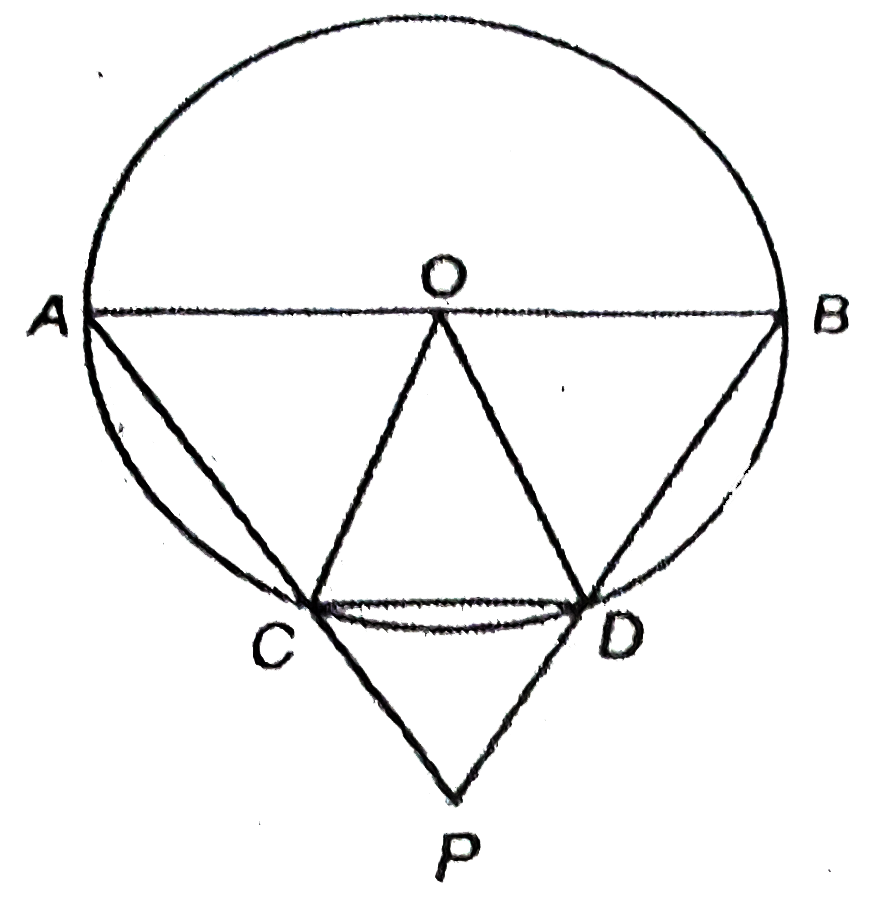 A60∘B30∘C90∘D160∘
A60∘B30∘C90∘D160∘
AB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.

View SolutionABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB=60∘ .
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionIn Figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘
View SolutionIn Fig. 10.32, AB is a diameter of the circle, CD is a chord equal to theradius of the circle. AC and BD when extended intersect at a point E. Prove that∠AEB = 60∘
View Solution
