1500 families with 2 children were selected randomly , and the following data were recorded.
Number of girls in a family210Number of families475814211
Compute the probability of a family , chosen at random , having
No girls. Also check whether the sum of these probabilities is 1.
The correct Answer is:2111500
To solve the problem, we will follow these steps:
Step 1: Identify the total number of families
The total number of families surveyed is given as 1500.
Step 2: Identify the number of families with no girls
From the data provided, the number of families with no girls (0 girls) is 211.
Step 3: Calculate the probability of a family having no girls
The probability P of a family having no girls can be calculated using the formula:
P(no girls)=Number of families with no girlsTotal number of families=2111500
Step 4: Calculate the probability of a family having one girl
The number of families with one girl is given as 814. Therefore, the probability of a family having one girl is:
P(one girl)=8141500
Step 5: Calculate the probability of a family having two girls
The number of families with two girls is given as 475. Therefore, the probability of a family having two girls is:
P(two girls)=4751500
Step 6: Check if the sum of all probabilities equals 1
We will sum the probabilities calculated in steps 3, 4, and 5:
P(no girls)+P(one girl)+P(two girls)=2111500+8141500+4751500
Combining these fractions:
=211+814+4751500=15001500=1
Conclusion
The probability of a family chosen at random having no girls is 2111500, and the sum of all probabilities is indeed 1.
---
The total number of families surveyed is given as 1500.
From the data provided, the number of families with no girls (0 girls) is 211.
The probability P of a family having no girls can be calculated using the formula:
P(no girls)=Number of families with no girlsTotal number of families=2111500
The number of families with one girl is given as 814. Therefore, the probability of a family having one girl is:
P(one girl)=8141500
The number of families with two girls is given as 475. Therefore, the probability of a family having two girls is:
P(two girls)=4751500
We will sum the probabilities calculated in steps 3, 4, and 5:
P(no girls)+P(one girl)+P(two girls)=2111500+8141500+4751500
Combining these fractions:
=211+814+4751500=15001500=1
The probability of a family chosen at random having no girls is 2111500, and the sum of all probabilities is indeed 1.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - Multiple Choice Questions (MCQs)10videos
PROBABILITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - Skill Testing Exercise8videos
PROBABILITY
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINE AND ANGLESEXERCISE - Multiple Choice Questions MCQs)10videos
LINE AND ANGLES
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS18videos
SURFACE AREAS AND VOLUMES
Similar Questions
1500 families with 2 children were selected randomly , and the following data were recorded.
Number of girls in a family210Number of families475814211
Compute the probability of a family , chosen at random , having
1 girlView Solution100 families with two children were selected randomly and the following data were recorded :
No. of girls in family210No. of families12808
Calculate the probability of a family chosen at random having
One girl.View Solution
Knowledge Check
- Question 1 - Select One
1500 families with 2 children each , were selected randomly and the following data were recorded .

Out of these families , one family is selected at random . What is the probability that the selected family has (i) 2 girls (ii) 1 girl , (iii) no girl ?A0.129 , 0.26 , 0.256B0.068 , 0.45 , 0.482C0.069 , 0.35 , 0.352D0.070 , 0.68 , 0.678
100 families with two children were selected randomly and the following data were recorded :
No. of girls in family210No. of families12808
Calculate the probability of a family chosen at random having
two girlsView Solution100 families with two children were selected randomly and the following data were recorded :
No. of girls in family210No. of families12808
Calculate the probability of a family chosen at random having
no girlView Solution1500 families with 2 children were selected randomly, and the following data were recorded:

Compute the probability of a family, chosen at random, having
1 girlView Solution1500 families with 2 children were selected randomly, and the following data were recorded:

Compute the probability of a family, chosen at random, having
2 girlsView Solution1500 families with 2 children were selected randomly, and the following data were recorded:

Compute the probability of a family, chosen at random, having
No girlView Solution1000 families with 2 children were selected randomly and the following data were recorded.
∣∣∣Number of boys in a family 0 1 2Number of families 140 560 300∣∣∣
If a family is chosen at random, find the probability that it has (i) no boy (ii) one boy (iii) two boys (iv) at least one boy (v) at most one boy.View Solution1500 families with 2 children were selected randomly and the following data were recorded:
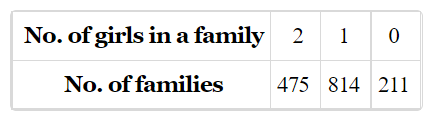
If a family is chosen at random, compute the probability that it has:
(i)No girl
(ii) 1 girl
(iii) 2 girls
(iv)at most one girlView Solution

