Activity : Note the frequency of two - wheelers , three - wheelers and four - wheelers going past during a time interval , in front of your school gate. Find the probability that any one vehicle out of the total vehicles you have observed is a two - wheeler.
To solve the problem of finding the probability that any one vehicle out of the total vehicles observed is a two-wheeler, follow these steps:
1. Assume Frequencies:
We will first assume the frequency of each type of vehicle. Let's say:
- Two-wheelers: 150
- Three-wheelers: 25
- Four-wheelers: 75
2. Create a Frequency Table:
We can organize the assumed frequencies in a table format for clarity:
|TypeofVehic≤|Frequency|⊢−−−−−−−−−−−−−−−−⊢−−−−−−−−||Two−whee≤r|150||Three−whee≤r|25||Four−whee≤r|75∣
3. Calculate Total Vehicles:
To find the total number of vehicles observed, we add the frequencies of all types of vehicles:
\(
\text{Total Vehicles} = 150 + 25 + 75 = 250
\)
4. Determine the Number of Two-Wheelers:
From our assumption, the number of two-wheelers is 150.
5. Calculate the Probability:
The probability \( P \) of selecting a two-wheeler from the total vehicles is given by the formula:
\(
P(\text{Two-wheeler}) = \frac{\text{Number of Two-wheelers}}{\text{Total Vehicles}} = \frac{150}{250}
\)
6. Simplify the Fraction:
We can simplify the fraction:
\(
\frac{150}{250} = \frac{3}{5}
\)
7. Conclusion:
Therefore, the probability that any one vehicle out of the total vehicles observed is a two-wheeler is:
\(
P(\text{Two-wheeler}) = \frac{3}{5}
\)
We will first assume the frequency of each type of vehicle. Let's say:
- Two-wheelers: 150
- Three-wheelers: 25
- Four-wheelers: 75
We can organize the assumed frequencies in a table format for clarity:
|TypeofVehic≤|Frequency|⊢−−−−−−−−−−−−−−−−⊢−−−−−−−−||Two−whee≤r|150||Three−whee≤r|25||Four−whee≤r|75∣
To find the total number of vehicles observed, we add the frequencies of all types of vehicles:
\(
\text{Total Vehicles} = 150 + 25 + 75 = 250
\)
From our assumption, the number of two-wheelers is 150.
The probability \( P \) of selecting a two-wheeler from the total vehicles is given by the formula:
\(
P(\text{Two-wheeler}) = \frac{\text{Number of Two-wheelers}}{\text{Total Vehicles}} = \frac{150}{250}
\)
We can simplify the fraction:
\(
\frac{150}{250} = \frac{3}{5}
\)
Therefore, the probability that any one vehicle out of the total vehicles observed is a two-wheeler is:
\(
P(\text{Two-wheeler}) = \frac{3}{5}
\)
Topper's Solved these Questions
- PROBABILITY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - Multiple Choice Questions (MCQs)
10 Videos
- PROBABILITY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - Skill Testing Exercise
8 Videos
- LINE AND ANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINE AND ANGLESEXERCISE - Multiple Choice Questions MCQs)
10 Videos
- SURFACE AREAS AND VOLUMESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS
18 Videos
Similar Questions
On a particular day, at a crossing in a city, the various types of 280 vehicles going past during a time interval were observed as under:
∣∣∣Type of vehicleTwo wheelersThree wheelersFour wheelersFrequency 91 63 126∣∣∣
Out of these vechicles , one is chosen at random, what is the probability that the chosen vechicle is
(i) a four wheeler
(ii) a two wheeler
(iii) a three wheeler?
View SolutionDirection: A vehicle manufacturing company sells three types of vehicles, 4 wheelers, 3 wheelers and 2 wheelers in two different sessions 2010-2012 and 2013-2015. In the first session, the ratio of 4 wheelers, 3 wheelers and 2 wheelers sold is 1 : 2 : 2. Also, 3 wheelers sold in this session is 20% more than the same type of wheelers sold in the second session. The total vehicles sold in session 2010-2012 is 12 lacs. The 4 wheelers sold in 2013-2015 is 20,000 more than the 2 wheelers sold in 2010-2012. The 2 wheelers sold in 2013- 15 are 12.5% more than that of sold in 2010-12.
If in session 2010-2012, the production of 4 wheelers and 2 wheelers are 2.8 lacs and 5 lacs, respectively, then find the ratio of unsold vehicles of the same type.
View Solution
Knowledge Check
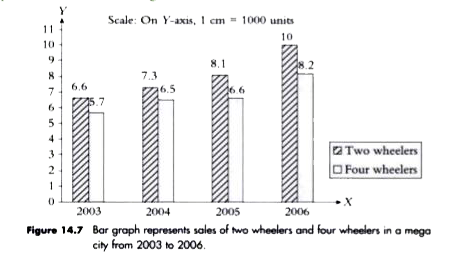
Find the maximum difference between sales of two wheelers and that of four wheelers, in any year, in the given period.A1500B1700C1800D2000There are twice the number of two wheelers as there are three wheelers and the number of four wheelers are equal to the number of two wheelers. The average of wheel per vehicle is :
A3B4C5Dnone of theseThere are twice the number of two wheelers as there are three wheelers and the number of 4 wheelers are equal to the number of two wheelers. The average number of wheel per vehicle is :
A3B4C5Dnone of these
On a particular day , at a crossing in a city , the various types of 240 vehicles going past during a time interval were observed as under :

Out of these vehicles , one is chosen at random . What is the probability that the chosen vehicle is a two-wheeler ?
View Solution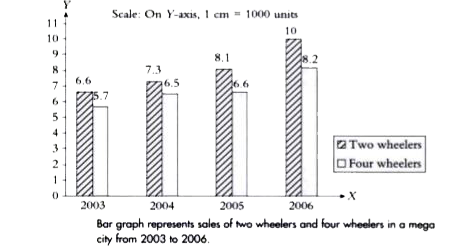
Total number of vehicles (two wheelers and four wheelers) sold in the years 2003 and 2004 is________
View SolutionIn a municipal parking there are some two wheelers and rest are 4 wheelers. If wheels are counted, there are total 520 wheels but the incharge of the parking told me that there are only 175 vehicles. If no vehicle has a stepney, then the no. of two wheelers is :
View SolutionIn a munciple parking thereare some two wheelers and rest are 4 wheelers. If wheels are counted, there are total 520 wheels but the incharge of the parking told me that there are only 175 vehicles. If no vehicle has a stepney, then the no. of two wheelers is :
View Solution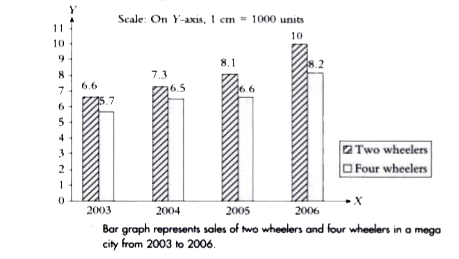
Find the total number of two wheelers sold in four years.
View Solution
