Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes :
Outcome321NoheadsheadsheadsheadsFrequency23727728
If the three coins are simultaneously tossed again , compute the probability of 2 heads coming up.
To solve the problem of finding the probability of getting 2 heads when three coins are tossed, we can follow these steps:
Step 1: Understand the problem
We are given the frequencies of different outcomes when three coins are tossed 200 times. The outcomes and their frequencies are:
- 3 heads: 23 times
- 2 heads: 72 times
- 1 head: 77 times
- No heads: 28 times
Step 2: Identify the total number of trials
The total number of times the coins were tossed is 200.
Step 3: Identify the favorable outcomes
We need to find the probability of getting exactly 2 heads. From the given data, the frequency of getting 2 heads is 72.
Step 4: Calculate the probability
The probability (P) of an event is given by the formula:
P(event)=Number of favorable outcomesTotal number of outcomes
In this case, the event is getting 2 heads. Thus, we can substitute the values:
P(2 heads)=72200
Step 5: Simplify the fraction
Now we simplify the fraction:
P(2 heads)=72÷8200÷8=925
Step 6: Final answer
The probability of getting exactly 2 heads when three coins are tossed is:
925
---
We are given the frequencies of different outcomes when three coins are tossed 200 times. The outcomes and their frequencies are:
- 3 heads: 23 times
- 2 heads: 72 times
- 1 head: 77 times
- No heads: 28 times
The total number of times the coins were tossed is 200.
We need to find the probability of getting exactly 2 heads. From the given data, the frequency of getting 2 heads is 72.
The probability (P) of an event is given by the formula:
P(event)=Number of favorable outcomesTotal number of outcomes
In this case, the event is getting 2 heads. Thus, we can substitute the values:
P(2 heads)=72200
Now we simplify the fraction:
P(2 heads)=72÷8200÷8=925
The probability of getting exactly 2 heads when three coins are tossed is:
925
Topper's Solved these Questions
- PROBABILITY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - Multiple Choice Questions (MCQs)
10 Videos
- PROBABILITY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - Skill Testing Exercise
8 Videos
- LINE AND ANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LINE AND ANGLESEXERCISE - Multiple Choice Questions MCQs)
10 Videos
- SURFACE AREAS AND VOLUMESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS
18 Videos
Similar Questions
Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes:
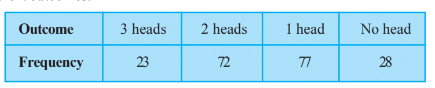
If the three coins are simultaneously tossed again, compute the probability of 2 heads coming up
View SolutionThree coins are tossed simultaneously 100 times with the following frequencies of different outcomes:
Outcome:NoheadOneheadTwoheadsThreeHeadFrequency:14383612
If the three coins are simultaneously tossed again, compute the probability of:
(i)2 heads coming up. (ii) 3 heads coming up. (iii)at least one head coming up. (iv)getting more heads than tails. (v)getting more tails than heads
View Solution
Knowledge Check
Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes.
∣∣∣Outcome3 heads2 heads1 headNo headFrequency 23 72 77 28∣∣∣
If the three coins are simultaneously tossed again, compute the probability of 2 heads coming up.A825B325C925D725Three coins are tossed simultaneously. What is the probability of getting no head ?
A18B14C38D34Three coins are tossed .Find the probability of no heads .
A38B18C12D23
Three coins are tossed simultaneously 100 times the following frequencies of different outcomes: Outcomes: No head One head Two heads Three head Frequency: 14 38 36 12 If the three coins are simultaneously tossed again, compute the probability of: (i) 2 heads coming up. (ii) 3 heads coming up. (iii) at least one head coming up. (iv) getting more heads than tails. (v) getting more tails than heads.
View SolutionThree coins are tossed simultaneously 200 times with the following frequencies of different outcomes.
∣∣∣Outcome3 heads2 heads1 headNo headFrequency 23 72 77 28∣∣∣
Find the probabiltiy of (i) getting at most two heads (ii) getting at least two heads.
View SolutionThree coins are tossed simultaneously 200 times with the following frequencies of different outcomes: Outcomes 3 heads 2 heads 1 head No head Frequency 23 72 77 28 Find the probability of getting at most two heads.
View SolutionIf two coins are tossed simultaneously. Find the probability of getting 2 heads.
View SolutionIn a simultaneous toss of two coins, find the probability of getting: 2 heads
View Solution
