A chain of length l and mass m lies on the surface of a smooth hemisphere of radius R>l with one end tied to the top of the hemisphere. Find gravitational potential energy of the chain with reference to the top of the hemisphere
The correct Answer is:−mR2gl
Similar Questions
A chain of length l and mass m lies on the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere.
View SolutionAS chain of length l and mass m lies o the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere. a.Find the gravitational potential energy of the chain with reference level at the centre of the sphere. B. suppose the chin is released and slides down the sphere. Find the kinetic eneergy of the chain, when it has slid through an angle θ c. find the tangential acceleration dvdt of the chain when the chain starts sliding down.
View Solution
Knowledge Check
A chain of length l=πR/4 is placed. On a smooth hemispherical surface of radius R with one of its ends fixed at the top of the sphere. Mass of chain is √πkg and R=1m.(g=10m/s2).
The gravitational potential energy of the chain considering reference level at the base of hemisphere isA20 JB20√2JC40 JD40√2JA chain of length l=πR/4 is placed. On a smooth hemispherical surface of radius R with one of its ends fixed at the top of the sphere. Mass of chain is √πkg and R=1m.(g=10m/s2).
If the chain sliped down the sphere, kinetic energy of the chain when it has sliped through an angle θ=π4.A23.4JB63.44JC80 JD97.4J
A chain of length l and mass m lies of the surface of a smooth hemisphere of radius R>l with one end tied to the top of the hemisphere. Taking base of the hemisphere as reference line, find the gravitational potential energy of the chain.
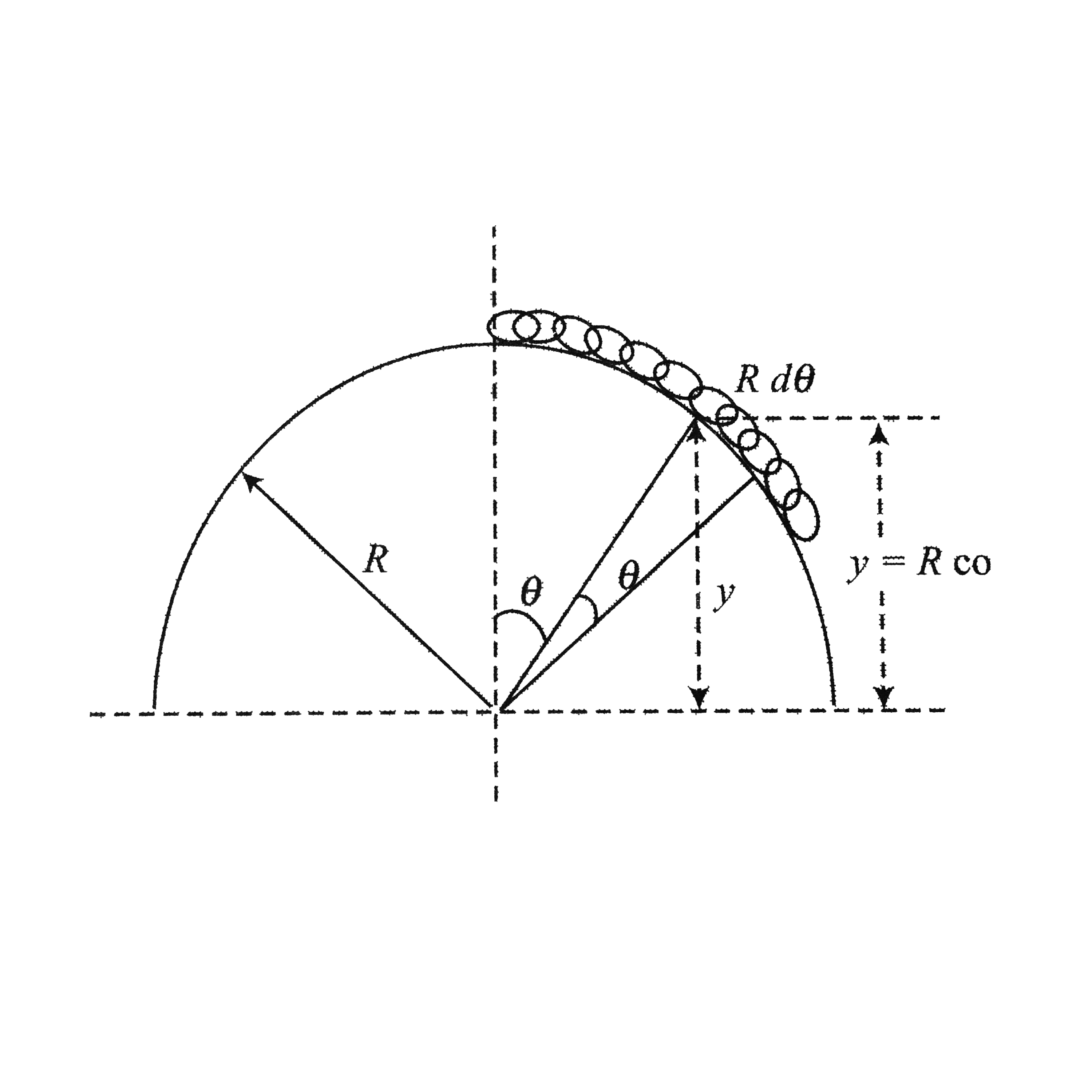
View SolutionA chain of length l and mass m lies of the surface of a smooth hemisphere of radius R>l with one end tied to the top of the hemisphere. Taking base of the hemisphere as reference line, find the gravitational potential energy of the chain.

View SolutionA uniform chain of mass m and length l<πR2 is placed on a smooth hemisphere of radius R with on of its ends fixed at the top of the sphere.
(a) Find the gravitational potential energy of chain assuming base of hemisphere as reference.
(b) what will be the tangential acceleraion of the chain when it starts sliding down.
(c ) If the chain slides down the sphere, find the kinetic energy of the chain when it has slipped through an angle β.
View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration of the each element of the chain when its upper end is released? It is assumed that the length of the chain l<(πR2).
View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain l<12πR.
View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain l<12πR.
View Solution
