A chain of mass m = 0.80 kg and length l = 1.5 m rests on a rough-surfaced table so that one of its ends hangs over the edge. The chain starts sliding off the table all by itself provided the overhanging part equals η=13 of the chain length. What will be the total work performed by the friction forces acting on the chain by the moment it slides completely off the table ?
The correct Answer is:−1.3 J
Similar Questions
A chain of mass m=0.80kg and length l=1.5m rests on a rough-surfaced table so that one of its ends hangs over the edge. The chain starts sliding off the table all by itself provided the overhanging part equals η=1/3 of the chain length. What will be the total work performed by the friction forces acting on the chain by the moment it slides completely off the table?
View SolutionA chain of mass m and length l rests on a roung surfced table so that one of its ends hangs over the edge. The chain starts sliding off the table all by itself provided the overhanging part equals 1/3of the chain length. What will be the total work performed by the fricition forces acting on the chain by the moment is slides completely off the table ? Friction cofficient is μ
View Solution
Knowledge Check
A chain of mass m and length l is placed on a table with one-sixth of it hanging freely from the table edge. The amount of work. done to pull the chain on the table is
Amgl/4Bmgl/6Cmgl/72Dmgl/36A chain of mass m and length l is placed on a table with one-sixth of it hanging freely from the table edge. The amount of work. done to pull the chain on the table is
Amgl/4Bmgl/6Cmgl/72Dmgl/36A uniform chain has a mass m and length l . It is held on a frictionless table with one - sixth of its length hanging over the edge. The work done in just pulling the hanging part back on the table is :
Amgl72Bmgl36Cmgl12Dmgl6
A uniform chain of mass m0 and length l rests on a rough incline with its part hanging vertically as shown in the fig. The chain starts sliding up the incline (and hanging part moving down) provided the hanging part equals η times the chain length (η lt 1). What is the work performed by the friction force by the time chain slides completely off the incline. Neglect the dimension of pulley and assume it to be smooth.
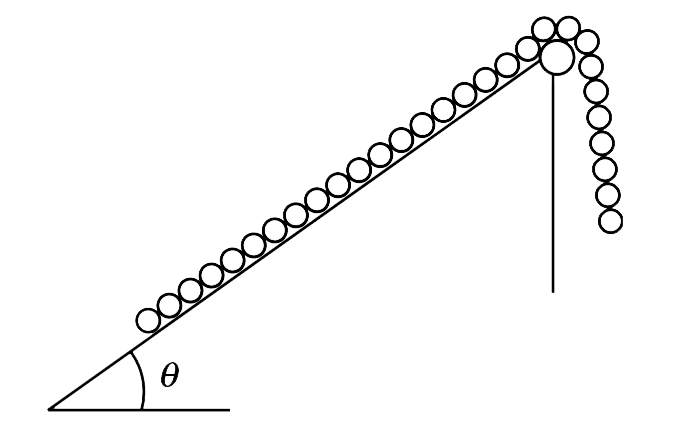
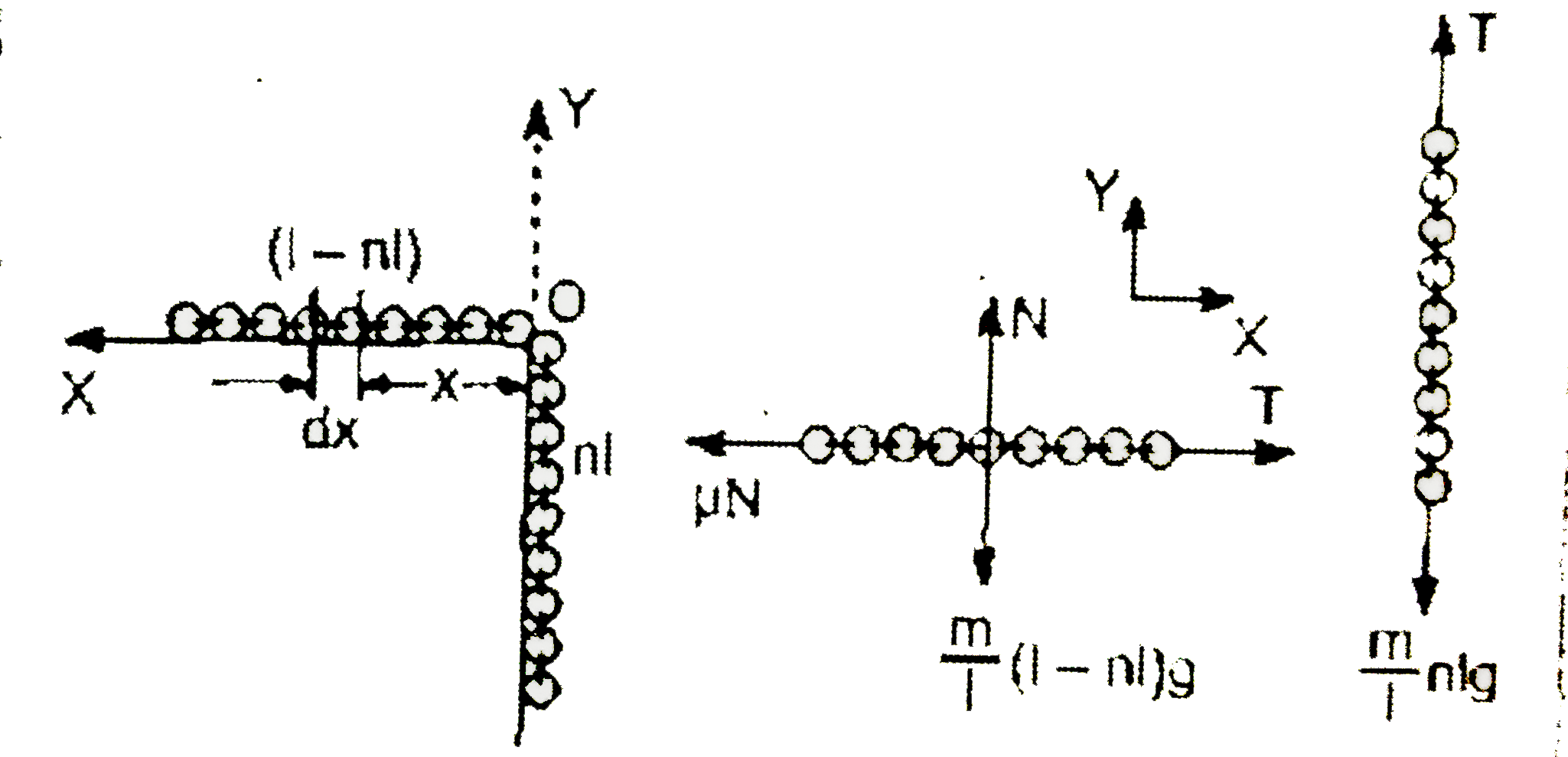
View SolutionA chain of mass m and length 1 lies on a rough table. The chain just starts to slip when the overhaning part equals nth fraction of the chain length. If the chain is slightly distributed so that it completely slips off the table, what is the work performed by the friction forces.
View SolutionA uniform chain of length l is placed on rough table with length l/n (where n>1) , hanging over the edge. If the chain just begins to slide off the table by itself from this position, the coefficient of friction between the chain and the table is
View SolutionA uniform chain of length l is placed on a rough table, with length l/3 hanging over the edge. If the chain just begins to slide off the table by itself from this portion, the coefficient of friction between the chain and the table is 1/K. Then find the value of K.
View SolutionA uniform chain of length l is placed on rough table with length l/n (where n>1) , hanging over the edge. If the chain just begins to slide off the table by itself from this position, the coefficient of friction between the chain and the table is
View Solution
