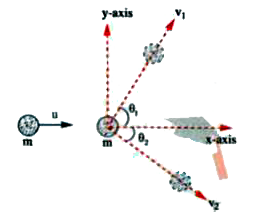
Prove that in case of oblique elastic collision of two particles of equal mass if one is at rest, the recoiling particles always move off at right angles to each other.

Text Solution

Verified by Experts

Method - I:
In elastic collision momentum is conserved, So, conservation of momentum along x-axis yields $m u = m v_{1} {cos θ}_{1} + m v_{2} {cos θ}_{2}, i . e ., u = v_{1} {cos θ}_{1} + v_{2} {cos θ}_{2} \dots . (1)$
and along y-axis yields, $0 = v_{1} sin t h e a_{1} - v_{2} {sin θ}_{2} ... . (2)$
Squaring and adding Eqns. (1) and (2), we get
$u^{2} = v_{1}^{2} + v_{2}^{2} + 2 v_{1} v_{2} cos (θ_{1} + θ_{2}) ... . . (3)$
As the collision is elastic $\frac{1}{2} m u^{2} = \frac{1}{2} m v_{1} + \frac{1}{2} m v_{2}^{2}$
$i . e ., u^{2} = v_{1}^{2} + v_{2}^{2} ... . (4)$
In the light of Eqn. (4), (3) reduces to
$2 v_{1} v_{2} cos (θ_{1} + θ_{2}) = 0$
As it is given that $v_{1} \neq 0 and v_{2} \neq 0$
so $cos (θ_{1} + θ_{2}) = 0 \Rightarrow (θ_{1} + θ_{2}) = 90^{\circ}$

Method -II:
In head on elastic collision between two particles, they exchange their velocities. In thsi case, the component of ball 1 along common normal direction, $v cos θ$

becomes zero after collision, wheile that of 2 becomes v $cos θ .$ While the components along common tangent directio of particles remain unchanged. Thus, the components along common tangent and common normal direction of both the balls in tabular form are given below.

From the above table and figure, we see that both the balls move at right angles after collision with velocities $v sin θ and v cos θ .$

Updated on:21/07/2023

A ball of mass m moving with a velocity v undergoes an oblique elastic collision with another ball of the same mass m but at rest. After the collision if the two balls move with the same speeds , the angle between their directions of motion will be:
A $30^{\circ}$
B $60^{\circ}$
C $120^{\circ}$
D $90^{\circ}$
A particle of mass m moving with velocity $\to V$ makes a head on elastic collision with another particle of same mass initially at rest. The velocity of the first particle after the collision will be
A $\to V$
B $- \to V$
C $- 2 \to V$
DZero
A particle of mass m moving with velocity $\to V$ makes a head on elastic collision with another particle of same mass initially at rest. The velocity of the first particle after the collision will be
A $\to V$
B $- \to V$
C $- 2 \to V$
Dzero