Three identical discs, A, B and C rest on a smooth horizontal plane as shown in figure. The disc A is set in motion with velocity v along the perpendicular bisector of the line BC joining the centres of the stationary discs. The distance BC between the centre of stationary discs B and C is n times the diameter .d. of each disc. At what value of n will the disc A recoil, stop and move on after elastic collision?
The correct Answer is:n≤√2,n=√2n>√2
Topper's Solved these Questions
- COLLISIONS BOOK - AAKASH SERIESCHAPTER - COLLISIONS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
4 Videos
- COLLISIONS BOOK - AAKASH SERIESCHAPTER - COLLISIONS EXERCISE - NUMERICAL EXERCISE ( LEVEL 1)
18 Videos
- CENTRE OF MASSBOOK - AAKASH SERIESCHAPTER - CENTRE OF MASSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED))
3 Videos
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - Questions for Descriptive Answers
10 Videos
Similar Questions
Three identical discs A,B and C rest on a smooth horizonal plane as shown in figure −40151. The disc A is set in motion with velocity b along the perpendicular bisector of the line BC joining the centres of the stationary discs. The distance BC joining the cnetes of the stationary disck B and C is n times the diameter of each disc. At what value of n will the disc A recoil, Stop, and move on after elastic collision. ?
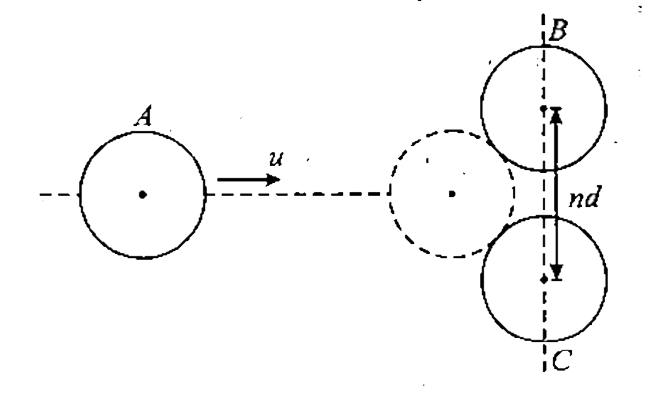
View SolutionThree identical discs A, B, and C (figure) rest on a smooth horizontal plane. The disc A is set in motion with vector v after which it experiences an elastic collision simultaneously with the discs B and C. The distance between the centres of the latter discs prior of the collision is η times greater than the diameter of each disc.
Find the velocity of the disc A after the collision. At what value of η will the disc A recoil after the collision, stop, move on?

View Solution
Knowledge Check
A small disc of radius 6 cm. If the distance between their centres is 3.2 cm, what is the shift in the centre of mass of the disc ?
A0.4 cmB2.4 cmC1.8 cmD1.2 cmA small disc of radius 6 cm. If the distance between their centres is 3.2 cm, what is the shift in the centre of mass of the disc ?
A0.4 cmB2.4 cmC1.8 cmD1.2 cmThe moment of Inertia of an incomplete disc of mas M and radius R as shown in figure about the axis passing through the centre and perpendicular to the plane of the disc is:
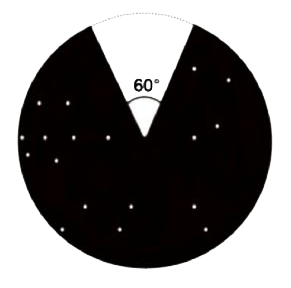 AMR22B7MR212C7MR26D5MR212
AMR22B7MR212C7MR26D5MR212
A small disc and a thin uniform rod of length l, whose mass is η times greater than the mass of the disc, lie on a smooth horizontal plane. The disc is set in motion, in horiozontal direction and perpendicular to the rod, with velocity v, after which it elastically collides with the end of the rod. Find the velocity of the disc and the angular velocity of the rod after the collision. At what value of η will the velocity of the disc after the collision be equal to zero? reverse its direction?
View SolutionA body of mass M (figure) with a small disc of mass m placed on it rests on a smooth horizontal plane. The disc is set in motion in the horizontal direction with velocity v. To what height (relative to the initial level) will the disc rise after breaking off the body M? The friction is assumed to be absent.
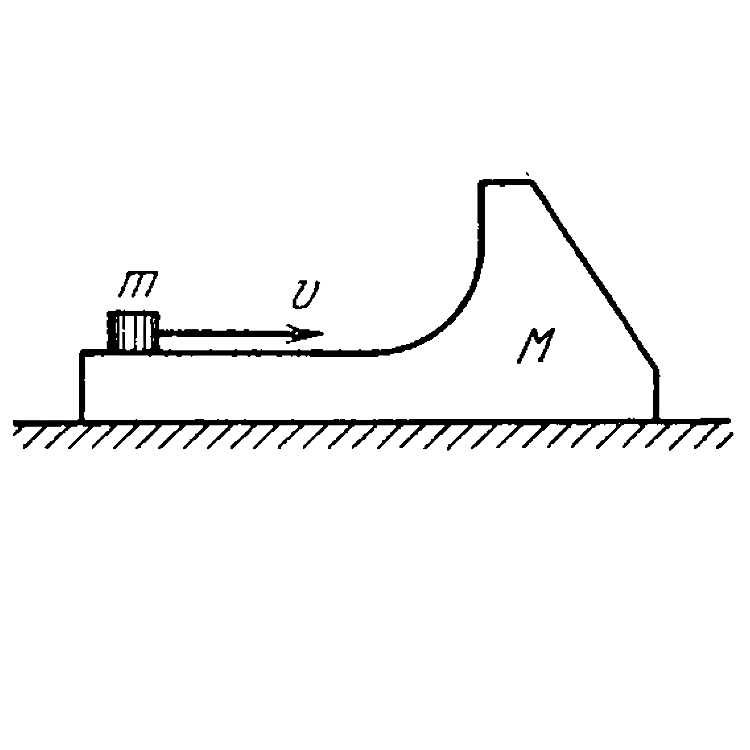
View SolutionA body of mass M (figure) with a small disc of mass m placed on it rests on a smooth horizontal plane. The disc is set in motion in the horizontal direction with velocity v. To what height (relative to the initial level) will the disc rise after breaking off the body M? The friction is assumed to be absent.

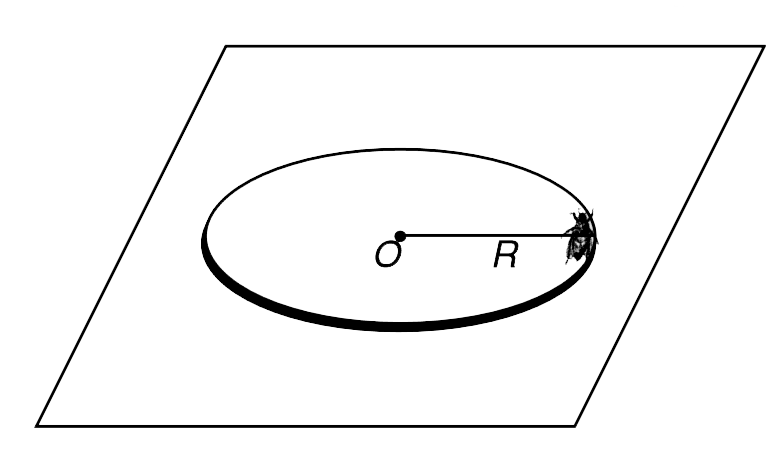
View SolutionA disc of mass M and radius R is kept flat on a smooth horizontal table. An insect of mass m alights on the periphery of the disc and begins to crawl along the edge.
(a) Describe the path of the centre of the disc.
For what value of mM the centre of the disc and the insect will follow the same path ?
View SolutionDisc A of radius R is lying flat on a horizontal surface. Disc B is also at rest. Disc C, which is identical to B is traveling along the surface with its velocity parallel to the line joining the centre C1andC2 of the discs A and B. The distance between the line C1C2 and the line of motion of centre of disc C is √3r , where r is radius of both B and C. Impact of C with B is completely elastic. Subsequently it is observed that both B and C just miss hitting the disc A. Find the radius (R) of A in terms of r.
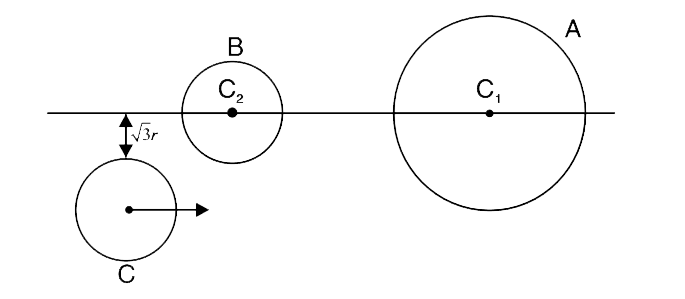
View Solution
