A body of mass M (figure) with a small disc of mass m placed on it rests on a smooth horizontal plane. The disc is set in motion in the horizontal direction with velocity v. To what height (relative to the initial level) will the disc rise after breaking off the body M? The friction is assumed to be absent.
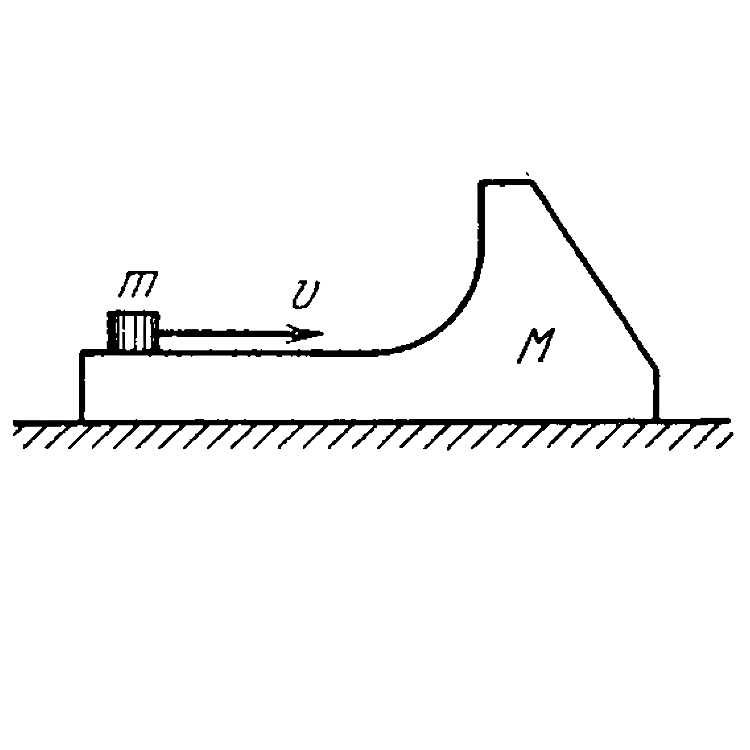
When the disc breaks off the body M, its velocity towards right (along x-axis) equals the velocity of the body M, and let the disc's velocity in upward direction (along y-axis) at that moment be
From conservation of momentum, along x-axis for the system (disc+body)
or
And from energy conservation, for the same system in the field of gravity:
,
where is the height of break off point from initial level. So,
, using (1)
or,
Also, if is the height of the disc, from the break-off point,
then,
So,
Hence, the total height, raised from the intital level
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation
34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body
56 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - The Fundamental Equation Of Dynamics
59 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
A body of mass M with a small block m placed on it rests on a smooth horizontal surface. The block is set in motion in the horizontal direction with a velocity v. To what height relative to the initial level will the block rise after breaking off from the body M. Friction can be assumed to be absent.

View SolutionA body of mass M with a small box of mass m placed on it rests on a smooth horizontal surface. The box is set in motion in the horizontal direction with a velocity u as shown in figure. To what height relative to the initial level will the box rise after breaking off from the body M? Assume all surfaces are frictionless.
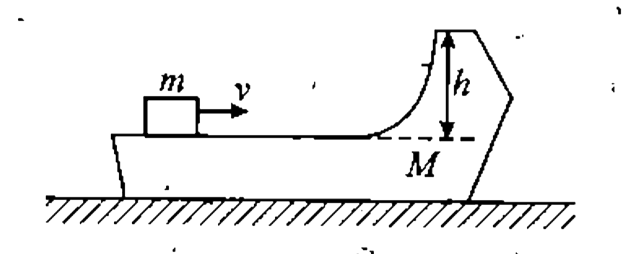
View Solution
Knowledge Check
A point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts
 A(2u3R)B(3u3R)C(5u3R)D(2u5R)
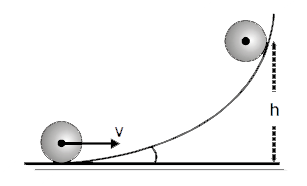
A(2u3R)B(3u3R)C(5u3R)D(2u5R)A disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:
 A3v22gB4v24gCv24gDv22g
A3v22gB4v24gCv24gDv22gDisc is rolling on the horizontal with constant If mass of the disc is velocity 2 m/s. 400 g, then total kinetic energy of disc is
A1.4 JB14 JC12 JD1.2 J
A small disc and a thin uniform rod of length l, whose mass is η times greater than the mass of the disc, lie on a smooth horizontal plane. The disc is set in motion, in horiozontal direction and perpendicular to the rod, with velocity v, after which it elastically collides with the end of the rod. Find the velocity of the disc and the angular velocity of the rod after the collision. At what value of η will the velocity of the disc after the collision be equal to zero? reverse its direction?
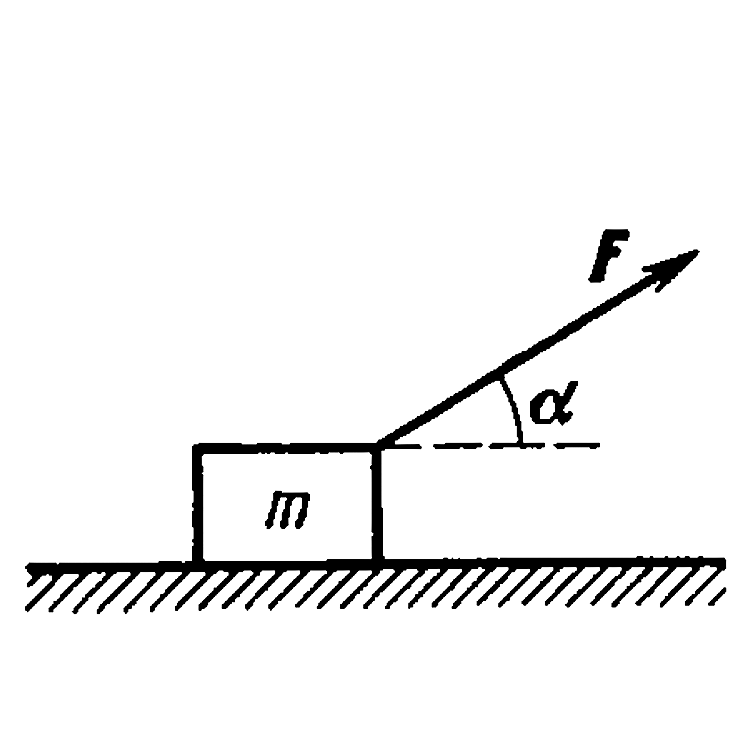
View SolutionAt the moment t=0 the force F=at is applied to a small body of mass m resting on a smooth horizontal plane (a is constant).
The permanent direction of this force forms an angle α with the horizontal (figure). Find:
(a) the velocity of the body at the moment of its breaking off the plane,
(b) the distance traversed by the body up to this moment.
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be :-
View SolutionTwo small discs of masses m1 and m2 interconnected by a weightless spring rest on a smooth horizontal plane. The discs are set in motion with initial velocities v1 and v2 whose directions are mutually perpendicular and lie in a horizontal plane. Find the total energy ˜E of this system in the frame of the centre of inertia.
View Solution
