A uniform lamina ABCDE is made from a square ABDE and an equilaterial triangle BCD. Find the centre of mass of the lamina.
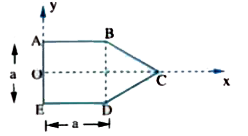
Here, A1= area of square ABDE =(a)(a) =a2
A2 = area of triangle =12(a)(√3a2)=√34a2
(x1,y1) = co-ordiantes of centre of mass of square =(a2,0)
(x2,y2) = co-ordinates of centre of mass of the triangle = (a+a2√3,0)
Now, xCM=A1x1+A2x2A1+A2=(a2).(a2)+√3a24(a+a2√3)a2+√34a2=0.74a
YCM=0 as y1 and y2 both are zero.
Therefore co-ordinates of CM of the given lamina are (0.74a, 0).
Similar Questions
Find the centre of mass of a uniform triangula lamina.
View SolutionFind the co-ordinates of centre of mass of the lamina shown in figure
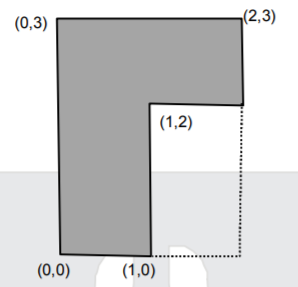
View SolutionFind the co-ordinates of centre of mass of the lamina shown in figure

View SolutionFind the co-ordinates of centre of mass of the lamina shown in figure

View SolutionFind the centre of mass of a uniform triangula lamina.
View SolutionWhat is the location of the centre of mass of a uniform triangular lamina ?
View SolutionFind the centre of mass of a uniform triangula lamina.
View SolutionFigure shows a right angled triangle of uniform mass per unit area, attached with rectangular lamina of sides 3m and 5m made of same material. Find the centre of mass of the system.

View SolutionFigure shows a right angled triangle of uniform mass per unit area, attached with rectangular lamina of sides 3m and 5m made of same material. Find the centre of mass of the system.

View SolutionFind the position of centre of mass of the uniform lamina shown in figure.
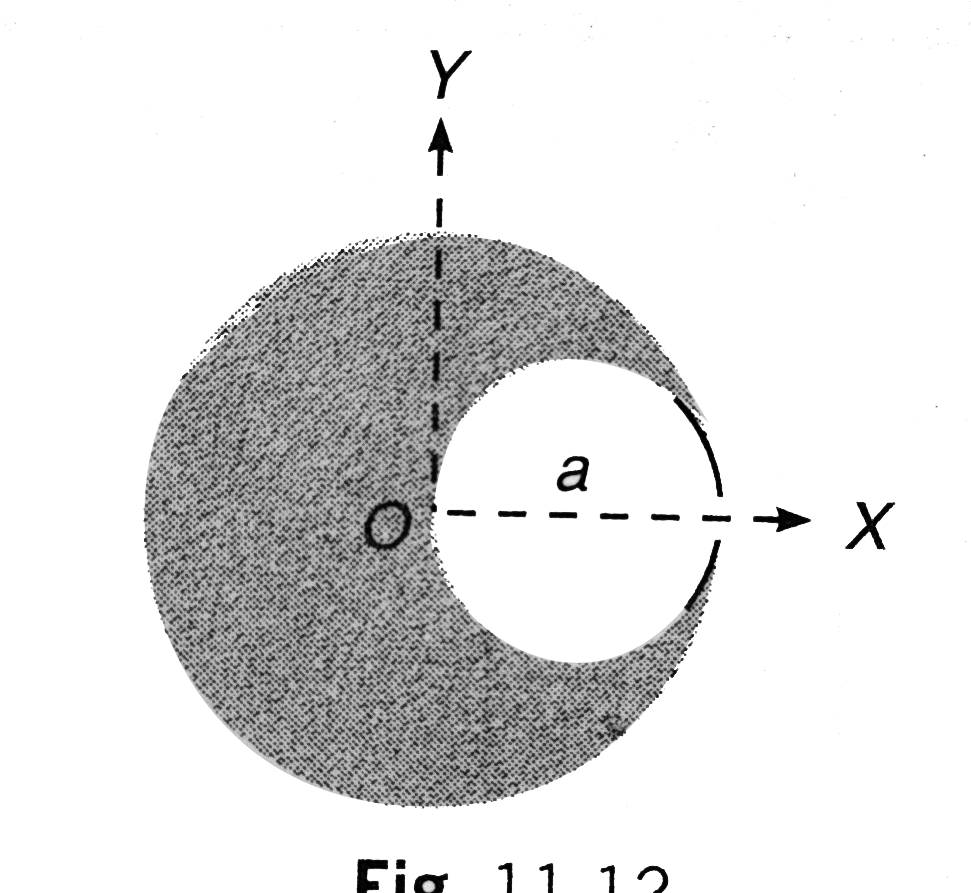
View Solution
